
Text erkannt:
Aufgabe 4 (10 Punkte). Sei \( a \in \mathbb{R} \) und \( c \in[0,1) \). Zeigen Sie, dass es genau eine stetig differenzierbare Funktion \( f:[0, c] \rightarrow \mathbb{R} \) gibt mit \( f(0)=a \) und
\( f^{\prime}(x)=\sin (f(x)) \text { für alle } \quad x \in[0, c] . \)
Ich weiß nicht genau wie ich diese formel anwende:
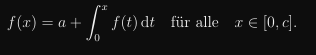
Text erkannt:
\( f(x)=a+\int \limits_{0}^{x} f(t) \mathrm{d} t \quad \) für alle \( \quad x \in[0, c] \).