Zeigen Sie, dass es genau eine stetig differenzierbare Funktion f:[0, c] → ℝ gibt mit f(0)=a und

Question

Text erkannt:

Aufgabe 4 (10 Punkte). Sei $a \in \mathbb{R}$ und $c \in[0,1)$. Zeigen Sie, dass es genau eine stetig differenzierbare Funktion $f:[0, c] \rightarrow \mathbb{R}$ gibt mit $f(0)=a$ und
$f^{\prime}(x)=\sin (f(x)) \text { für alle } \quad x \in[0, c] .$

Ich weiß nicht genau wie ich diese formel anwende:

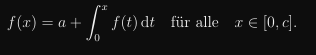
Text erkannt:

$f(x)=a+\int \limits_{0}^{x} f(t) \mathrm{d} t \quad$ für alle $\quad x \in[0, c]$.

Comments

Diese Aufgabe ist hier schon in Arbeit.