Aufgabe:
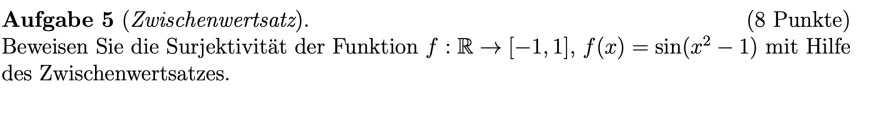
Text erkannt:
Aufgabe 5 (Zwischenwertsatz). \( \quad \) (8 Punkte) Beweisen Sie die Surjektivität der Funktion \( f: \mathbb{R} \rightarrow[-1,1], f(x)=\sin \left(x^{2}-1\right) \) mit Hilfe des Zwischenwertsatzes.
Hallo Zusammen, ich hänge momentan an dieser Aufgabe.
Meine Idee: (grob)
Ich würde die Umkehrfunktion f-1:[-1, 1] →ℝ betrachten und dann jeweils 2 Intervalle [a,b] = [-1,0] und [c,d] = [0, 1].
Nach dem Zwischenwertsatz existiert dann ein x0∈D mit f-1(0) <= f-1(x0) <= f-1(-1) (analog Intervall [0,1]).
da f-1(0) = 0, und f-1(1)= \( \frac{π}{2} \) (analog -1), existieren beispielsweise zwei x∈ℝ, sd. f(x) )= \( \frac{π}{2} \).
So wie ich das verstehe, ist es so, dass für jedes x∈[a,b] und y ∈[c,d] mit -x=y f-1(x) = z = f-1(y) (z∈ ℝ)gilt, also ein Element (z) aus ℝ mit f(z) auf x und y Abbildet. Daraus würde ja dann Surjektivität folgen.
Meine Frage ist, welche Rolle der Zwischenwertsatz bei dieser Erkenntnis hat und, wie man durch ihn die Surjektivität erklären kann?
Vielen Dank!
(Die Frage existiert bereits, allerdings erklären die Antworten meine Frage nicht)