Zeigen Sie: Für die Wronski-Determinante gilt W(\varphi_{1}, \varphi_{2})(x)=c e^{-\int p(x) {d} x}, c ∈ ℝ .

Question

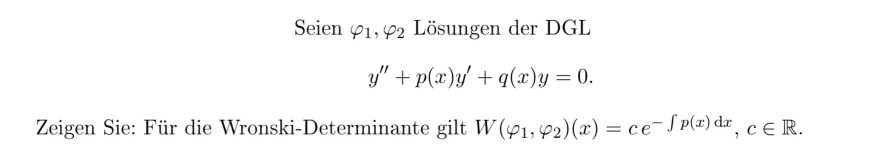
Text erkannt:

Seien \( \varphi_{1}, \varphi_{2} \) Lösungen der DGL
\( y^{\prime \prime}+p(x) y^{\prime}+q(x) y=0 . \)
Zeigen Sie: Für die Wronski-Determinante gilt \( W\left(\varphi_{1}, \varphi_{2}\right)(x)=c e^{-\int p(x) \mathrm{d} x}, c \in \mathbb{R} \).

Hallo,

hat jemand einen Ansatz für mich, ich bin mit Matrizen und Determinanten nicht so fit und weiß nicht, wo genau ich da die Wronski-Determinante anwenden soll. Ich danke jedem, der mir hilft

LG Noel

Comments

(Ich würde zur Vereinfachung erstmal u und v statt der phi nehmen.)

Wie ist W(u,v) definiert - explizit, nach Auswertung der Determinante? Bilde die Ableitung von W(u,v). Benutze die Differentialgleichung, um in der Ableitung von W(u,v) die zweiten Ableitungen u ersetzen ....

Answer 1

Hallo,

................................