Jakobi Matrix mit Verkettung

Question

Aufgabe:

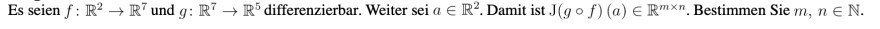
Text erkannt:

Es seien \( f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{7} \) und \( g: \mathbb{R}^{7} \rightarrow \mathbb{R}^{5} \) differenzierbar. Weiter sei \( a \in \mathbb{R}^{2} \). Damit ist \( \mathrm{J}(g \circ f)(a) \in \mathbb{R}^{m \times n} \). Bestimmen Sie \( m, n \in \mathbb{N} \).

Problem/Ansatz:

Ich bräuchte bei dieser Aufgabe dringend Hilfe. Mein Ansatz wäre, dass man für f 2 Variablen zB x1, x2 hat und einen 7-Zeiligen Vektor hat. und für g dasselbe nur mit 7 Variablen und 5 Zeiligem Vektor. Aber weiter komme ich nicht. Ich weiß nicht wie ich die Verkettung durchführen soll, und was für m und n am Ende rauskommt.

Answer 1

Du brauchst hier keine Verkettung durchführen, Du musst Dir nur überlegen, was Definitions- und Wertebereich von \(g\circ f\) ist, genauer \(\mathbb{R}\) hoch wieviel? Dann ist die Größe von \(J\) sofort klar.

Comments

Ich komme dabei auf 5x2.

---

Fast. In der ersten Spalte von \(J\) stehen immer die Ableitungen der ersten Funktion nach den versch. Variablen.

---

Also ich bin jetzt folgendermaßen vorgegangen. Da g∘f steht habe ich g(f(a)) angenommen. Ich dachte dann, dass die Variablen von g mit denen von f also 2 ersetzt werden (wie bei der Verkettung:

). Somit käme man auf 2 Variablen aus f und die 5 Funktionen von g. Die Anzahl der Zeilen wäre die Anzahl der Zeilen und die Anzahl der Spalten die Anzahl der möglichen partiellen Ableitungen, was ja bei 2 Variablen auch 2 entspricht. Daher die 5x2.

---

Ach, sorry, da hab ich gepennt. Du hast vollkommen recht. 5x2 stimmt.

---

Danke für die Hilfe :)

---

Gerne, und sorry für die Verwirrung. In der ersten Spalte von \(J\) stehen natürlich alle Ableitungen nach der ersten Variablen, ergibt 5 Zeilen und 2 Spalten.