Wahrscheinlichkeit Intervall bestimmen

Question

Aufgabe:

Die Abb. F.3 zeigt den Graph einer normalverteilten Zufallsgröße X.

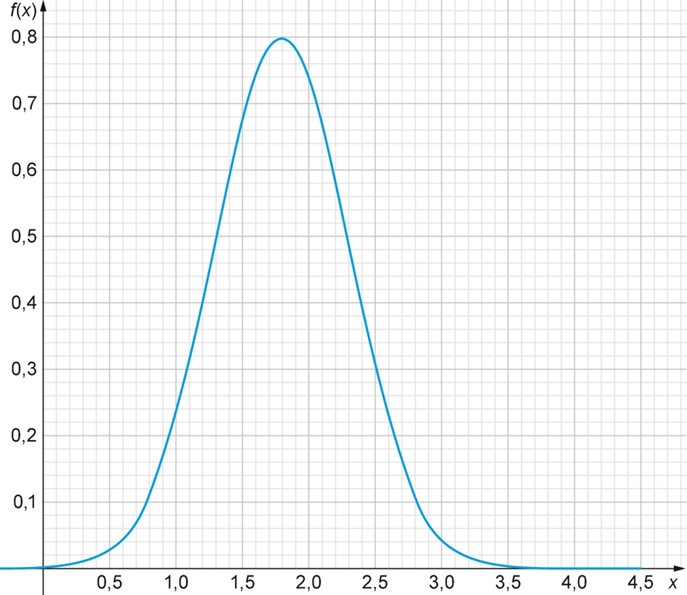
Abb. F.3: Normalverteilte Zufallsgröße X
a) Geben Sie den Erwartungswert der Zufallsgröße an.
b) Geben Sie die Wahrscheinlichkeit für X = 1,2 an.
c) Bestimmen Sie die Wahrscheinlichkeit dafür, dass X einen Wert aus dem Intervall [2,1; 2,6] annimmt.

Problem/Ansatz:

Aufgabe a) und b) habe ich bereits... ich hoffe das ist richtig... aber bei c) weiß ich nicht, was ich für x nehmen soll..:

Für μ würde ich 1,8 nehmen und für σ 0,5... ist das richtig?

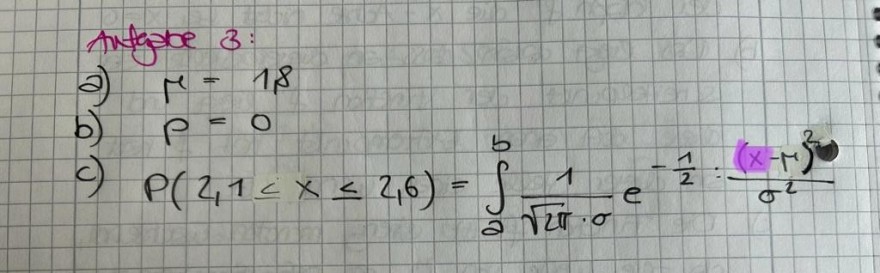
Text erkannt:

Antabre 3:
a) \( \mu=18 \)
b) \( p=0 \)
c) \( P(2,1 \leq x \leq 2,6)=\int \limits_{a}^{b} \frac{1}{\sqrt{2 \pi} \cdot \sigma} e^{-\frac{1}{2} \cdot \frac{(x-\mu)^{2}}{\sigma^{2}}} \)

Answer 1

Ich glaube nicht, dass man hier \(\sigma\) ablesen/bestimmen soll.

Wenn du dir aber die Punkte auf dem Graphen für \(x=2.1\) und \(x=2.6\) anschaust, siehst du, dass zwischen diesen beiden Punkten der Graph sehr gut durch ein Geradenstück approximiert wird.

Du liest die Punkte ab:

$$(2.1\,|\; 0.66),\: (2.6\,|\; 0.22)$$

Jetzt bestimmst du die Fläche des Trapezes zwischen dem Geradenstück und der \(x\)-Achse:

$$P(2.1 \leq X \leq 2.6)\approx \frac 12\left(0.66 + 0.22\right)\cdot (2.6-2.1)= 0.22$$

Answer 2

a) und b) hätte ich genau so gelöst.

Bei c) sollst du nur eine Fläche bestimmen

Berechne zunächst dafür die Standardabweichung und nutze dann die Normalverteilung zum berechnen der Fläche. Ich komme dabei auf ca. 22%. Ich denke das sollte näherungsweise langen.

Comments

Welche Zahl hast du für X eingesetzt? Als Standardabweichung habe ich 0,5.

Das wäre mein Ansatz:

Text erkannt:

\( \int \limits_{2,1}^{2,6} \frac{1}{\sqrt{2 \pi \times 0,5}} \times e^{-\frac{1}{2} \times \frac{(1,2-1,8)^{2}}{0,5^{2}}} d x \)
\( \begin{array}{l}\frac{\sqrt[50]{\mathbf{\pi}^{\mathbf{2 5}} \mathbf{e}^{\mathbf{1 4}}}}{\mathbf{2} \mathbf{e} \mathbf{\pi}} \\ \approx 0,13731\end{array} \)

---

Interessent ist ja das in deinem Integral gar kein x mehr auftaucht.

Wenn da kein x auftaucht dann braucht man auch nicht aufwendig ein Integral bilden oder?

---

Naja, bei -1/2^(X-1,8)^2 kommt das X vor und ich habe für das X 1,2 eingesetzt, weil ich nicht wusste, was ich dort einsetzten soll...

---

Da bleibt einfach das x stehen. Aber eigentlich hat jeder bessere Taschenrechner Funktionen für die Normalverteilung integriert. Und zur Not gibt es auch Tabellen zum nachschlagen.