Berechnen Sie das Taylorpolynom

Question

Aufgabe: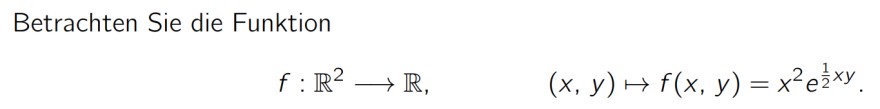

Text erkannt:

Betrachten Sie die Funktion
$f: \mathbb{R}^{2} \longrightarrow \mathbb{R}, \quad(x, y) \mapsto f(x, y)=x^{2} e^{\frac{1}{2} x y}$

Text erkannt:

Berechnen Sie das Taylorpolynom
$T_{2}(\cdot, p): \mathbb{R}^{2} \longrightarrow \mathbb{R}, \quad z \mapsto T_{2}(z, p)=\sum \limits_{\substack{\alpha \in \mathbb{N}_{0}^{2} \\|\alpha| \leq 2}} \frac{\partial^{\alpha} f(p)}{\alpha !}(z-p)^{\alpha}$
im Punkt $p=(1,1)$.

Problem/Ansatz:

Wie ist das z zu Interpretieren?

Answer 1

z ist das, was sonst meist (x,y) heißt. Eine Variable, die genauso gut (u,v) oder sonstwie heißen könnte. Einsetzen und ausrechnen, steckt nichts groß dahinter, was zu interpretieren wäre.