Gleichung auflösen nach x / F

Question

Aufgabe:

Gleichung auflösen nach \( \frac{x}{F} \)

Problem/Ansatz:

Ich stoße aktuell bei Auflösung der Gleichung (siehe Anhang) an meine mathematischen Grenzen.

Die Gleichung muss nach \( \frac{x}{F} \) aufgelöst werden.

Ich ersuche höflichst um Unterstützung bei der Lösung

Vielen Dank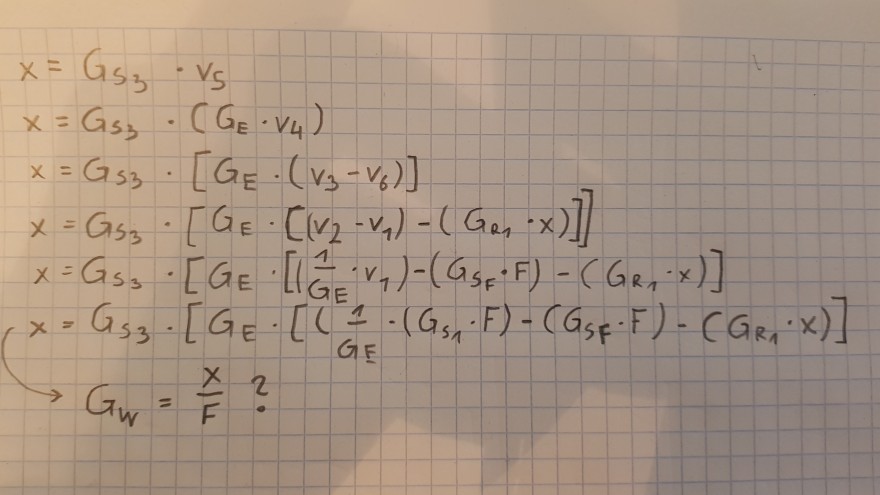

Text erkannt:

\( \begin{array}{l}x=G_{S_{3}} \cdot v_{S} \\ x=G_{S_{3}} \cdot\left(G_{E} \cdot v_{4}\right) \\ x=G_{S_{3}} \cdot\left[G_{E} \cdot\left(v_{3}-v_{6}\right)\right] \\ x=G_{S_{3}} \cdot\left[G_{E} \cdot\left[\left(v_{2}-v_{1}\right)-\left(G_{R_{1}} \cdot x\right)\right]\right] \\ x=G_{S_{3}} \cdot\left[G_{E} \cdot\left[\left(\frac{1}{G_{E}} \cdot v_{1}\right)-\left(G_{S_{F}} \cdot F\right)-\left(G_{R_{1}} \cdot x\right)\right]\right. \\ x=G_{S_{3}} \cdot\left[G_{E} \cdot\left[\left(G_{1} \cdot\left(G_{S_{1}} \cdot F\right)-\left(G_{S_{F}} \cdot F\right)-\left(G_{R_{1}} \cdot x\right)\right]\right.\right. \\ \rightarrow G_{W}=\frac{x}{F} ?\end{array} \)

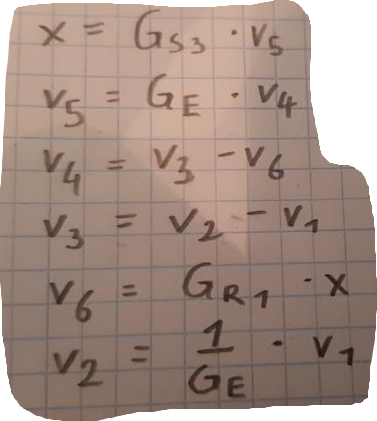
Text erkannt:

\( \begin{array}{l}x=G_{53} \cdot v_{5} \\ v_{5}=G_{E} \cdot v_{4} \\ v_{4}=v_{3}-v_{6} \\ v_{3}=v_{2}-v_{1} \\ v_{6}=G_{R_{1}} \cdot x \\ v_{2}=\frac{1}{G_{E}} \cdot v_{1}\end{array} \)

Answer 1

Schau mal, ob das so passt

$$x = G_{S3}·v_5 \newline x = G_{S3}·G_E·v_4 \newline x = G_{S3}·G_E·(v_3 - v_6) \newline x = G_{S3}·G_E·(v_2 - v_1 - G_{R1}·x) \newline x = G_{S3}·G_E·(\frac{1}{G_E}·v_1 - v_1 - G_{R1}·x) \newline x = G_{S3}·v_1 - G_{S3}·G_E·v_1 - G_{S3}·G_E·G_{R1}·x \newline x + G_{S3}·G_E·G_{R1}·x = G_{S3}·v_1 - G_{S3}·G_E·v_1 \newline x·(1 + G_{S3}·G_E·G_{R1}) = G_{S3}·v_1·(1 - G_E) \newline x = \frac{G_{S3}·v_1·(1 - G_E)}{1 + G_{S3}·G_E·G_{R1}} \newline x = \frac{G_{S3}·G_{SF}·F·(1 - G_E)}{1 + G_{S3}·G_E·G_{R1}} \newline \frac{x}{F} = \frac{G_{S3}·G_{SF}·(1 - G_E)}{1 + G_{S3}·G_E·G_{R1}}$$