Hallo Fiona,
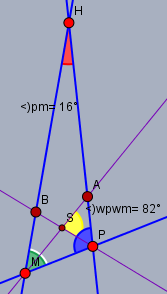
der Winkel bei \(M\) sei \(\alpha\) (grün) und der bei \(P\) sei \(\beta\) (blau). Der Schnittpunkt der Winkelhalbierenden (lila) sei \(S\). Die Winkelsumme im Dreieck \(\triangle MPS\) ist$$\frac{1}{2}\alpha + \frac{1}{2}\beta + (180° - 82°) = 180° \\ \implies \alpha + \beta = 2 \cdot 82° = 164°$$und aus der WInkelsumme im Dreieck \(\triangle MPH\) folgt der Winkel \(\angle MHP\)*) (rot)$$\angle MHP = 180° - 164° = 16°$$*) Bem.: genau genommen ist \(\angle PHM = 360° - 16° \)!
Gruß Werner