Zu einer Funktion den richtigen Funktionsgraphen ankreuzen

Question

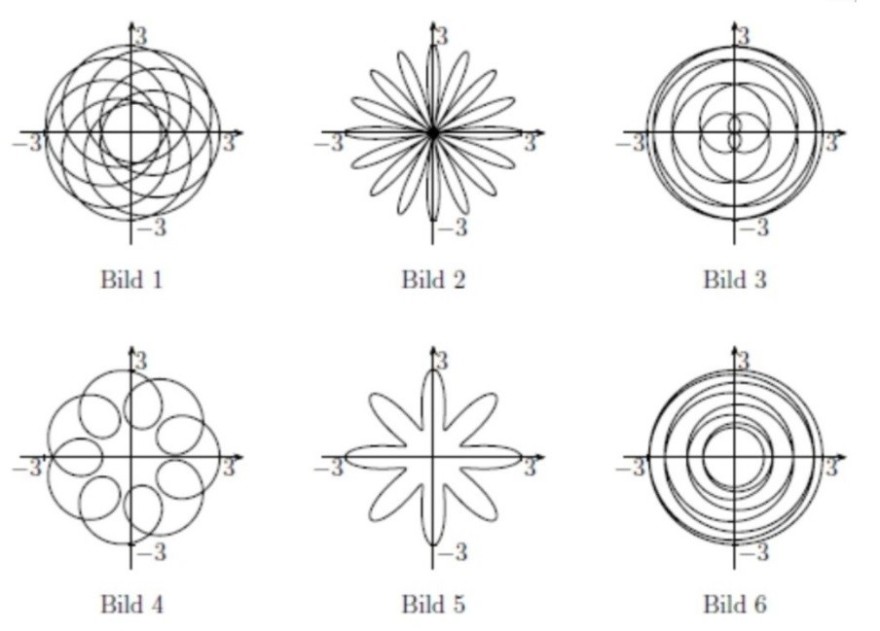
könnte mir jemand bitte erklären, wie er/sie bei dieser Aufgabe vorgehen würde?

Wir sollen zu einer Funktion den richtigen Funktionsgraphen ankreuzen. Erlaubt ist ein "einfacher Taschenrechner", also kein Grafikrechner o.ä. Der Casio, den ich habe, kann zwar keine solve-Funktion, allerdings habe ich hier mit einer Tabelle gearbeitet.

Mit den Nullstellen, die ich herausbekommen habe, habe ich sie dann in x(t) (s.u.) eingesetzt.

Konkret also:

Gegeben ist: $$ (2 + cos(8t)) *   \begin{pmatrix} cos(t)\\sin(t) \end{pmatrix} $$

Das habe ich unterteilt in x(t) = (2 + cos(8t)) * cos(t) und y(t) = (2 + cos(8t)) * sin(t)

Dann y(t) = 0 -> bei 0 ist eine Nullstelle (herausgefunden mit der "Table" Funktion beim Casio TR)

Diese dann in x(t) eingesetzt, kommt also x(0) = 3.

So, weiter komme ich nun nicht mehr, da sowohl Bild 2 als auch Bild 5 infrage kommt. Wie würdet ihr hier weitermachen?

Comments

Hallo,

mit desmos sieht es so aus:

https://www.desmos.com/calculator/rswpkyp9iz

:-)

Answer 1

Während eines Kreisumlaufes

\( \begin{pmatrix} cos(t)\\sin(t) \end{pmatrix} \)

Schwanken die Funktionswerte 8 mal zwischen 3 und 1

\( (2 + cos(8t)) \)

Das erkennst du auf Bild 5.

In Bild 2 schwanken die Funktionswerte zwischen 0 und 3 wenn du genau schaust. Und wir haben 16 wechsel zwischen 3 und 0. Dann wäre der Funktionsterm

\( (1.5 + 1.5 \cdot cos(16t)) *  \begin{pmatrix} cos(t)\\sin(t) \end{pmatrix} \)

Comments

Verstehe, danke!

Gibt es eigentlich eine Möglichkeit, diese Aufgabe ohne einen TR zu lösen?
Oder anders gefragt: Was ist die schnellste Methode, diese Aufgabe zu lösen?
Für diese Aufgabe hätte ich nämlich nur 6 Minuten, was bei 3 versch. Funktionen und bei 6 versch. Funktionsgraphen viel zu wenig (für mich) ist.

---

Wenn du die die beiden Faktoren anschaust aus denen das Produkt aufgebaut ist dann erkennst du das was ich oben gesagt hatte auf den ersten Blick.

Probiere mal mit Geogebra zu erkennen welchen Funktionsterm die anderen Funktionen haben.

Bild 1 vermutlich so, obwohl mir das in der Mitte zu eckig aussieht.