Differenzialgleichung gegeben - Lösung ankreuzen, zu der der folgende Graph eine Lösung darstellt

Question

Hallo,

folgende 2 Teilaufgaben kann ich leider nicht ganz lösen, ich habe es selbst probiert und es hat nicht geklappt.

Dann habe ich versucht, es Geogebra zeichnen zu lassen - allerdings ohne Erfolg (ist die Aufgabe womöglich falsch)?

a)

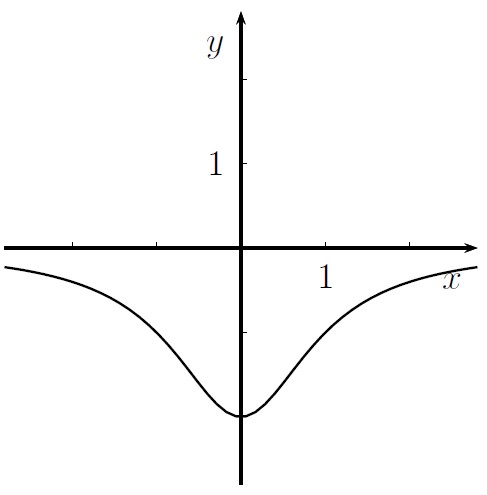
Kreuzen Sie diejenige Differenzialgleichung an, zu der der folgende Graph eine Lösung darstellt. Kreuzen Sie weiter an, welche Anfangsbedingungen für das entsprechende Anfangswertproblem möglich sind.

Zur Auswahl stehen:
y' = x²y
y' = -x²y
y' = -xy²
y' = xy²

y(1) = -1
y(-1) = -1
y(0) = 4
y(-2) = 3

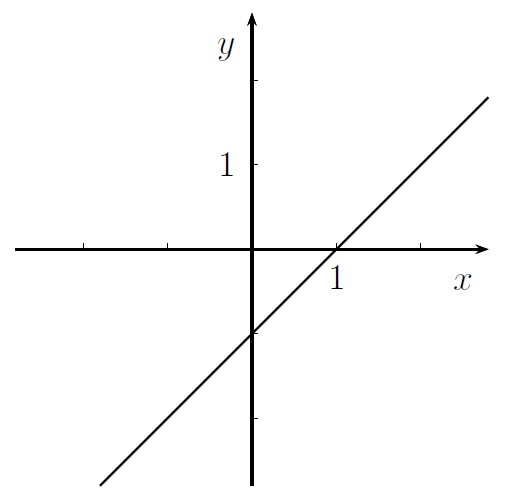
b)

Zur Auswahl stehen:

y' = x + y
y' = x - y
y' = -y - x
y' = y - x

y(1) = 0
y(2) = 4
y(0) = 4
y(-1) = -2

Answer 1

Hallo

wenn du dir die Steigungen  und funktionswerte  des Graphen ansiehst  x<0  negativ, y auch negativ also , und x>0 Steigung positiv, x auch negativ  kommt x^2  als Faktor von y' nicht in Frage  ,

wenn überhaupt dann y'= xy^2 weil dann die Vorzeichen der Ableitung stimmen  und wenn man y' bildet bei x=1, y=-1 stimmt auch die Steigung und y'' ein Wendepunkt

b) da der Graph y=x-1 , also y'=1  folgt y=-y+x

Gruß lul

Comments

Ich habe oben geschrieben, was zur Auswahl steht.
Ich kann da eigene eigenen Werte eingeben

---

Hallo

ich versteh den Kommentar nicht. ich hab doch je einen aus den vieren dir gezeigt?

was meinst du mit "Ich kann da eigene eigenen Werte eingeben"

lul

---

bei b) hast du geschrieben:
"y' = 1"

Diese Lösung steht nicht zur Auswahl

---

Hallo

ich hatte das 1=-y+x dazugeschrieben, y'=1 ergibt der Graph von y=x-1

lul