Die gespannte Schnur liegt maximal 196,2 m unter dem Meeresspiegel.

Text erkannt:
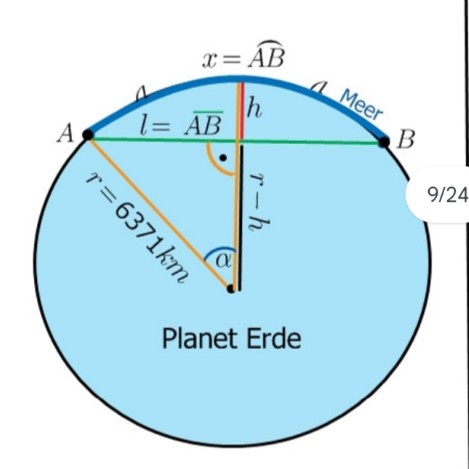
Eine Schnur wird vom Küstenpunkt A bis zum Punkt B (jew auf Höhe des Meeresspiegels) gespannt. Der Weg von A ne \( B \) entlang der Erdkrümmung betrage \( x=\overline{A B}=100 \mathrm{~km} \). Wi weit liegt die Schnur maximal unterhalb des Meeresspiegel Man berechne auch die Länge I \( =\overline{\mathrm{AB}} \) der Schnur.
\( \frac{x}{r \pi}=\frac{2 \alpha}{180} \Leftrightarrow \alpha=\frac{90 x}{r \pi}=0,44966^{\circ} \)
\( \begin{array}{l} h \text { berechnen: } \\ \cos \alpha=\frac{r-h}{r} \\ r \cos \alpha=r-h \\ h=r-r \cos \alpha \\ h=r(1-\cos \alpha) \\ h=0,1962 \mathrm{~km} \\ h=196,2 \mathrm{~m} \end{array} \)
el.
lberechnen:
\( \begin{aligned} \sin \alpha & =\frac{l}{2 r} \\ l & =2 r \sin \alpha \\ l & =99,9988 \mathrm{~km} \end{aligned} \)
\( x-l=0,0012 k m=1,2 r \)
Die gespannte Schnur ist un kürzer als der Weg von A na der Erdkrümmung.
Aufgabe:
Problem/Ansatz:
Hey folgendes Problem ich versteh wie man auf h und l kommt, aber leider komme ich leider nicht drauf wie man auf die 0,44 grad kommt
Könnte mir jemand das Schritt für Schritt erklären?
Ich hab keine Ahnung wie man auf die Formel kommt und wie diese abgeleitet wird
Vielen dank