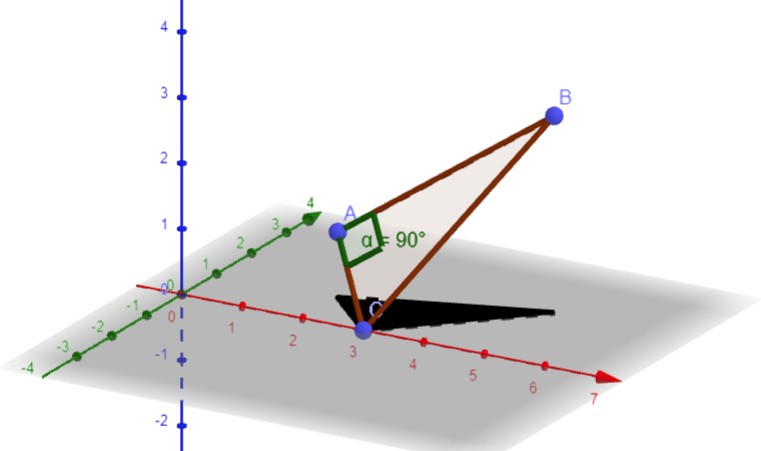
A(2|1|1), B(5|2|3), C(3|0|0)
Stelle die Richtungsvektoren auf
AB = B - A = [5,2,3] - [2,1,1] = [3,1,2]
AC = C - A = [1,-1,-1]
Zwei Vektoren sind senkrecht, wenn ihr Skalarprodukt 0 ist
AB * AC = [3,1,2] * [1, -1,-1] = 3 + (-1) + (-2) = 0
Damit ist der Winkel bei A 90 Grad und das Dreieck ist rechtwinklig.
Skizze