Aufgabe:
Bei der Messung der Betondeckung an verschiedenen Stellen eines Bauteils erhielt man folgende Werte (in mm): \( \begin{array}{lllllll}4,5 & 3,6 & 3,8 & 4,1 & 3,2 & 3,9 & 4,2\end{array} \)
a) Berechnen Sie den Mittelwert und die Standardabweichung.
b) Geben Sie das \( 98 \% \) Konfidenzintervall für den Erwartungswert \( \mu \) an. (Falls Aufgabenteil a) nicht bearbeitet wurde, sind \( \bar{x}=3,5 \mathrm{~mm} \) und \( \mathrm{s}=0,41 \mathrm{~mm} \) anzunehmen. Hinweis: Diese Werte sind nicht zur Überprüfung von Aufgabenteil a) geeignet!)
Problem/Annsatz:
a) \( \bar{x}=3.9 \mathrm{~mm} ; s=0.42 \mathrm{~mm} \)
b) \( P\left\{3.402 \mathrm{~mm} \leq \mu \leq 4.398 \mathrm{~m} \mathrm{~m}_{y}\right\}=98 \% \)
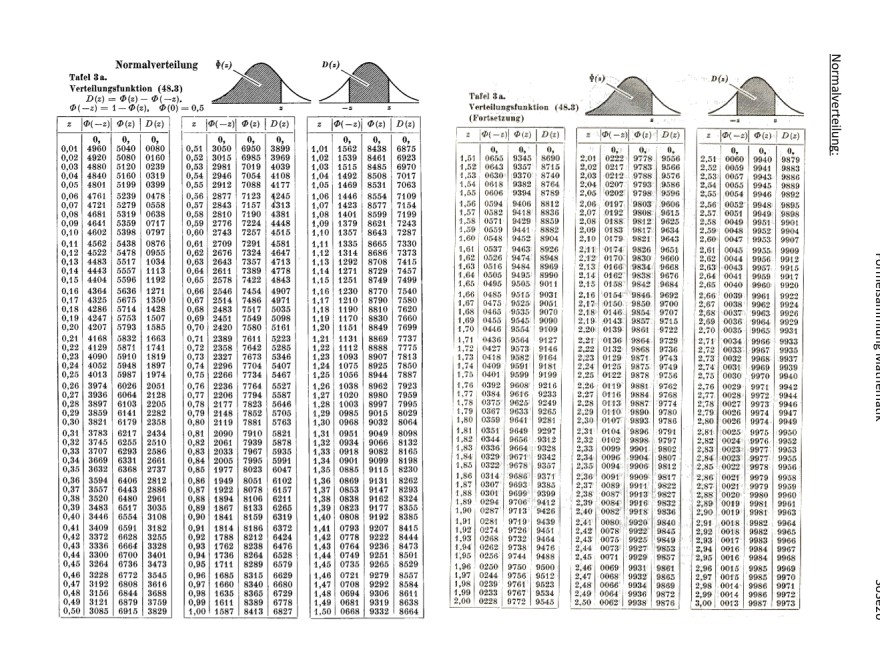
Hallo zusammen, bei Aufgabenteil b komme ich leider nicht weiter. ich weiß nicht welchen wert aus der Tabelle für mich relevant ist und wie ich damit dann weiter rechne um auf das unter der Aufgabe stehende Ergebnis zu kommen. Für Unterstützung wäre ich sehr dankbar.