Dichtefunktion der Normalverteilung

Question

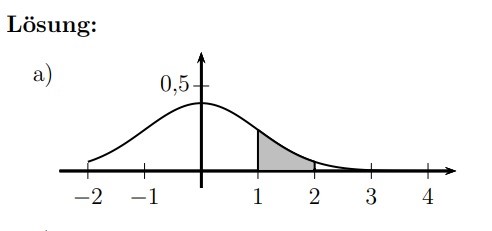
Aufgabe:

Skizzieren Sie in einem Koordinatensystem die Wahrscheinlichkeitsdichten zu Normalverteilungen mit

a) µ = 0, σ = 1.

Wie groß ist jeweils die Wahrscheinlichkeit eines Ereignisses im Intervall [1;2] ?

Problem/Ansatz:

Woher weiß man, dass der Graph den Hochpunkt bei knapp unter 0,5 hat? Wieso der bei dieser x-Achse den Hochpunkt hat (µ = 0) ist mir schon klar. Ebenfalls, dass man durch σ = 1 jeweils eins nach rechts und links geht, bevor dann der Fall kommt, auch.

Bild zum Graphen:

Comments

man durch σ = 1 jeweils eins nach rechts und links geht, bevor dann der Fall kommt

Diese Aussage ist nicht nachvollziehbar. Die Dichte fällt links und rechts vom Modus, also bei x = 0, und nicht erst bei x = ± 1.

Answer 1

Vermutlich kennst du die Dichtefunktion der Normalverteilung

$$f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \cdot e^{-\frac{(x - \mu)^2}{2 \sigma^2}}$$

Ist also sie Standardabweichung 1 erhältst du beim einsetzen des Erwartungswertes

$$\frac{1}{\sqrt{2 \pi}} = 0,3989$$

Also sind das etwa 0,4.

Comments

"e hoch x"

Was wäre denn hier in diesem Fall das x?

---

x ist dann der Erwartungswert. In der Standardnormalvereiung also x = μ = 0

Letztendlich steht dort aber dann nur e^0 = 1. Also rechnest du dann nur das was vor dem e-Term steht aus.

---

Alles klar, dankeschön!

---

Wenn x = μ ist die also das gleiche sind, wieso schreibt man dann überhaupt x - μ?

Das hebt sich doch wieder auf?

Wenn μ = 5 ist z.B. dann hätte man 5-5. Also kommt da doch immer eine 0 raus!

---

x ist doch nur im Hochpunkt gleich μ. An allen anderen Stellen ist x ≠ μ. Du hast doch beim Graphen nur keine einen Hochpunkt.