Aufgabe:
Bestimme das charakteristische Polynom der folgenden Matrix.
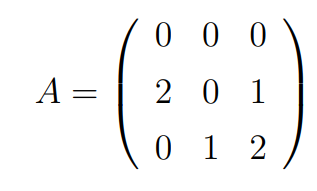
Text erkannt:
\( A=\left(\begin{array}{lll}0 & 0 & 0 \\ 2 & 0 & 1 \\ 0 & 1 & 2\end{array}\right) \)
Problem/Ansatz:
Mir ist klar, dass ich die Determinante bestimmen sollte (ich mache das mit dem Satz von Sarrus), aber ich bekomme einen Fehler sobald ich es vereinfache. Hier ist meine falsche Lösung:
det(A-s)= (2-s)*(-s)*(-s)+0*1*0+0*2*1-0*(-s)*0-1*1*(-s)-(2-s)*2*0 = (-s)^2*(2-s)+s
In der Lösung steht jedoch: −t(t^2 − 2*t − 1)
Wo liegt mein Fehler?