Guten Morgen,
erst einmal vielen Dank für die Rückmeldung!
Ich habe nun die Koeffizienten a0, an und bn bestimmt und daraus die Fourierreihe gebildet.
Bei a0 bin ich zuversichtlich, dass mein Ergebnis korrekt ist, bei an und bn jedoch nicht (bei beidem erhalte ich als Ergebnis 0).
Ich wäre sehr dankbar, wenn du/ ihr mal drüber schaut, ggf. Korrekturen vornehmt, bzw. die eigenen Ergebnisse der Aufgabe angebt.
Vielen Dank im Voraus!
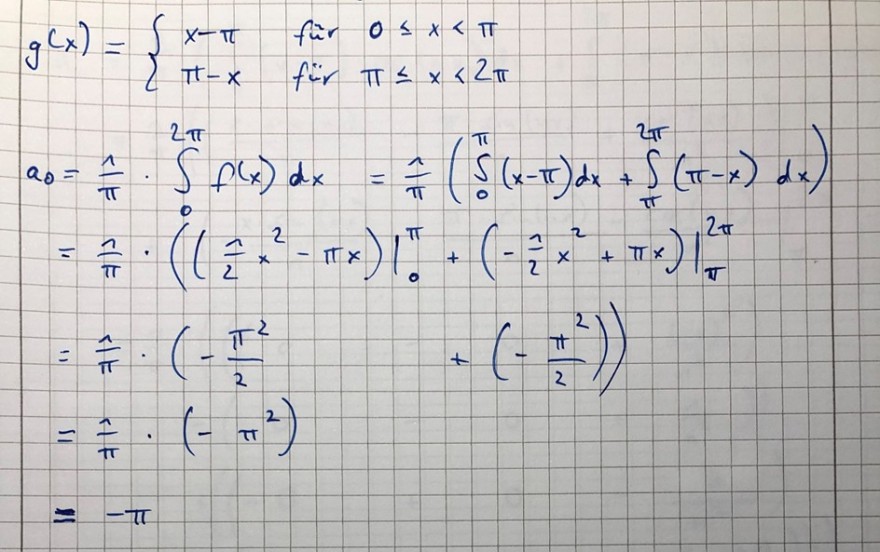
Text erkannt:
\( \begin{aligned} g(x) & =\left\{\begin{array}{ll}x-\pi & \text { für } 0 \leq x<\pi \\ \pi-x & \text { für } \pi \leq x<2 \pi\end{array}\right. \\ a_{0} & =\frac{1}{\pi} \cdot \int \limits_{0}^{2 \pi} f(x) d x=\frac{1}{\pi}\left(\int \limits_{0}^{\pi}(x-\pi) d x+\int \limits_{\pi}^{2 \pi}(\pi-x) d x\right) \\ & =\frac{1}{\pi} \cdot\left(\left.\left(\frac{1}{2} x^{2}-\pi x\right)\right|_{0} ^{\pi}+\left.\left(-\frac{1}{2} x^{2}+\pi x\right)\right|_{\pi} ^{2 \pi}\right. \\ & =\frac{1}{\pi} \cdot\left(-\frac{\pi^{2}}{2}+\left(-\frac{\pi^{2}}{2}\right)\right) \\ & =\frac{1}{\pi} \cdot\left(-\pi^{2}\right) \\ & =-\pi\end{aligned} \)
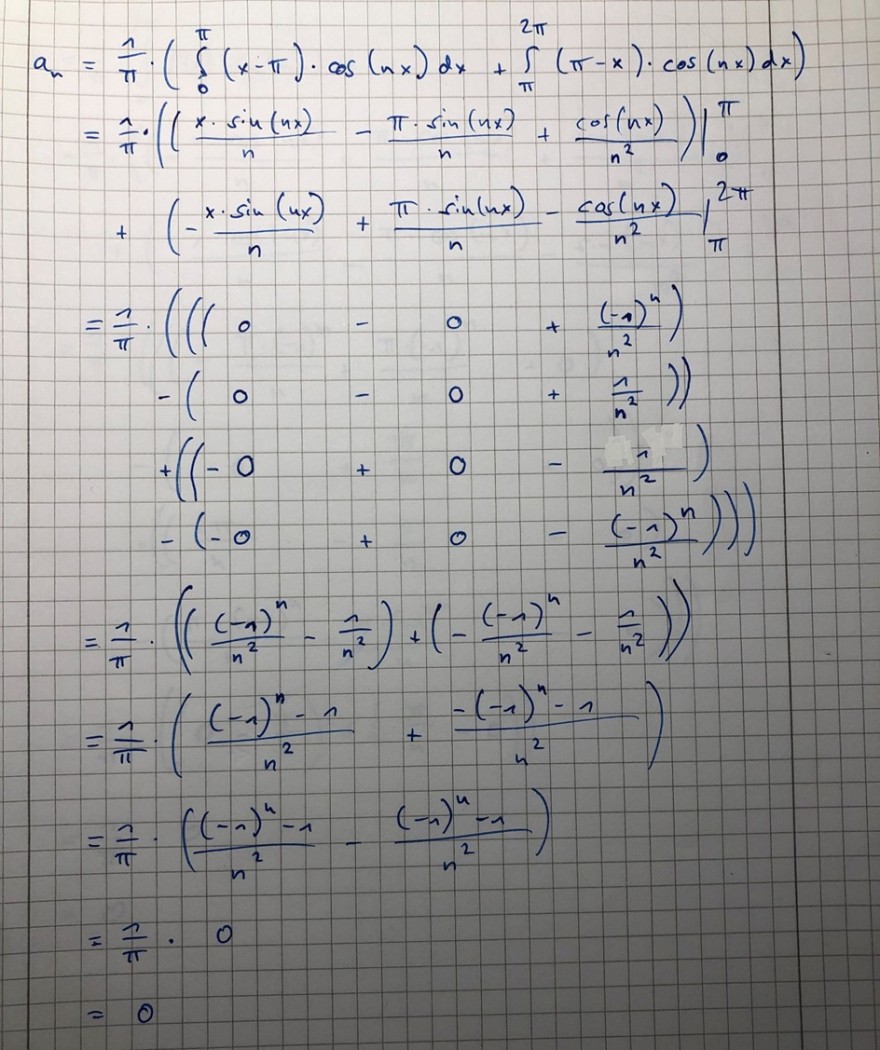
Text erkannt:
\( \begin{array}{l}a_{n}=\frac{1}{\pi} \cdot\left(\int \limits_{0}^{\pi}(x-\pi) \cdot \cos (n x) d x+\int \limits_{\pi}^{2 \pi}(\pi-x) \cdot \cos (n x) d x\right) \\ =\frac{\hat{\pi}}{\pi} \cdot\left(\left.\left(\frac{x \cdot \sin (n x)}{n}-\frac{\pi \cdot \sin (n x)}{n}+\frac{\cos (n x)}{n^{2}}\right)\right|_{0} ^{\pi}\right. \\ +\left(-\frac{x \cdot \sin (n x)}{n}+\frac{\pi \cdot \sin (n x)}{n}-\left.\frac{\cos (n x)}{n^{2}}\right|_{\pi} ^{2 \pi}\right. \\ =\frac{1}{\pi} \cdot\left(\left(\begin{array}{ll}\left.0+0+\frac{(-1)^{n}}{n^{2}}\right) \\ -1\end{array}\right)\right. \\ \left.-\left(0-0+\frac{1}{n^{2}}\right)\right) \\ +\left(\left(-0+0-\frac{1}{n^{2}}\right)\right. \\ \left.\left.-\left(-0+0-\frac{(-1)^{n}}{n^{2}}\right)\right)\right) \\ =\frac{1}{\pi} \cdot\left(\left(\frac{(-n)^{n}}{n^{2}}-\frac{1}{n^{2}}\right)+\left(-\frac{(-1)^{n}}{n^{2}}-\frac{1}{n^{2}}\right)\right) \\ =\frac{1}{\pi} \cdot\left(\frac{(-1)^{n}-1}{n^{2}}+\frac{-(-1)^{n}-1}{n^{2}}\right) \\ =\frac{1}{\pi} \cdot\left(\frac{(-n)^{n}-1}{n^{2}}-\frac{(-n)^{n}-n}{n^{2}}\right) \\ =\frac{1}{\pi} \cdot 0 \\ =0 \\\end{array} \)

Text erkannt:
\( \begin{aligned} b_{n}= & \frac{1}{\pi} \cdot \int \limits_{0}^{2 \pi} f(x) \cdot \sin (n x) d x \\ = & \frac{1}{\pi} \cdot\left(\left.\left(-\frac{x \cdot \cos (n x)}{n}+\frac{\pi \cdot \cos (n x)}{n}+\frac{\sin (n x)}{n^{2}}\right)\right|_{0} ^{\pi}\right. \\ & +\left.\left(\frac{x \cdot \cos (n x)}{n}-\frac{\pi \cdot \cos (n x)}{n}-\frac{\sin (n x)}{n^{2}}\right)\right|_{\pi} ^{2 \pi} \\ = & \frac{1}{\pi} \cdot\left(\left(\left(-\frac{\pi \cdot(-1)^{n}}{n}+\frac{\pi \cdot(-1)^{n}}{n}+0\right)\right.\right. \\ & -(0)+0)) \\ & \left.+\left(\left(\frac{2 \pi}{n}+\frac{\pi}{n}-0\right)\right)\right) \\ & -\left(\frac{\pi \cdot(-1)^{n}}{n}-\frac{\pi \cdot(-n)^{n}}{n}\right. \\ = & \frac{1}{\pi} \cdot\left(\left(0-\frac{\pi}{n}\right)+\left(\frac{\pi}{n}-0\right)\right) \\ = & \frac{1}{\pi} \cdot(0 \\ = & 0\end{aligned} \)

Text erkannt:
tusarmengetruy un \( a_{0}, a_{n}, b_{n} \) :
\( \begin{aligned} F_{f}(x) & =\frac{a_{0}}{2}+\sum \limits_{n=1}^{\infty}\left(a_{n} \cdot \cos (n x)+b_{n} \cdot \sin (n x)\right) \\ & =\frac{-\pi}{2}+0 \\ & =-\frac{\pi}{2} \end{aligned} \)