Nullstellenform bei ganzrationalen Funktionen

Question

Hallo, ich habe zwei Fragen im Bezug auf ganzrationale Funktionen und deren Nullstellen.

Ich habe im folgenden Anhang versucht die Nullstellen der Funktion -x3+6x2-9x herauszufinden. Und anschließend die Nullstellenform zu bilden. Dabei scheint meine Nullstellenformm nicht korrekt zu sein. Da ein anderer Graf als beim ursprünglichen Funktionsterm rauskommt. Könnte mir jemand weiterhelfen, den Fehler zu finden.

Zudem würde ich gerne wissen wie ich jetzt weiß, das die 3 eine doppelte Nullstellen ist.

Vielen Dank schon mal

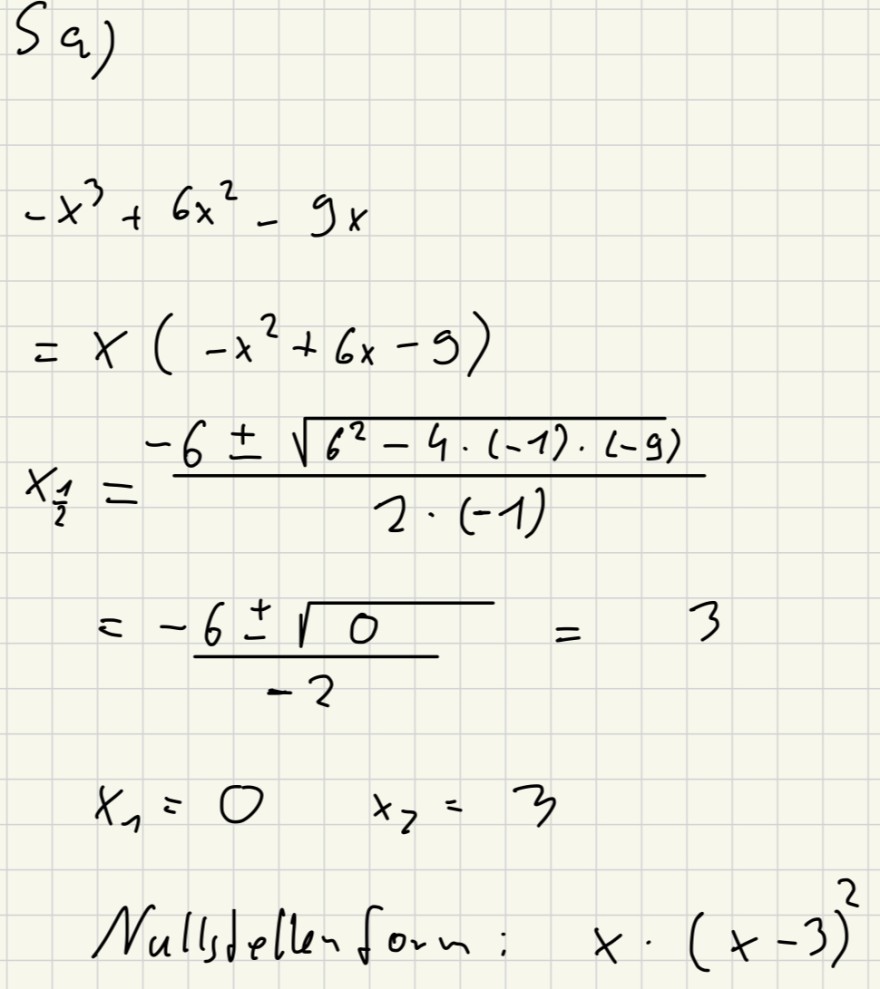
Text erkannt:

\( S a) \)
\( \begin{array}{l} -x^{3}+6 x^{2}-9 x \\ =x\left(-x^{2}+6 x-9\right) \\ x_{\frac{1}{2}}=\frac{-6 \pm \sqrt{6^{2}-4 \cdot(-1) \cdot(-9)}}{2 \cdot(-1)} \\ =\frac{-6 \pm \sqrt{0}}{-2}=3 \\ x_{1}=0 \quad x_{2}=3 \\ \text { Nullsdellenforn: } \quad x \cdot(x-3)^{2} \end{array} \)

Answer 1

Nullstellen der Funktion -x³+6x²-9x herauszufinden. Und anschließend die Nullstellenform zu bilden.

Nullstellenform von

        \(ax^3 + bx^2 + cx\)

lautet

        \(a(x-x_1)(x-x_2)(x-x_3)\).

wobei \(x_1\), \(x_2\) und \(x_3\) die Nullstellen sind.

In deinem Fall ist \(a = -1\), \(x_1 = 0\) und \(x_2=x_3=3\).

Dabei scheint meine Nullstellenformm nicht korrekt zu sein.

Sie ist es nicht, weil ein anderer Graph als beim ursprünglichen Funktionsterm rauskommt.

Wie unterscheiden sich die Graphen?

wie ich jetzt weiß, das die 3 eine doppelte Nullstellen ist.

Es ist

        \(x^2 - 6x + 9 = (x-3)^2\)

laut binomischer Formel.

Comments

Text erkannt:

\( f(x)=-x^{3}+6 x^{2}-9 x \)
\( g(x)=x(x-3)^{2} \)
+ Eingabe...

---

Beschreibe in Worten, wie der ursprüngliche Graph aus deinem Graphen erzeugt werden kann.

Tipp. In der EF wurden im Mathematikunterricht sogenannte Funktionstransformationen besprochen.

---

Danke für die Mühe!

Answer 2

\( f(x)=-x^{3}+6 x^{2}-9 x \)

\( f´(x)=-3x^{2}+12 x-9 \)

\(-3x^{2}+12 x-9=0   |:(-3) \)

\(x^{2}-4 x+3=0  \)

\(x^{2}-4 x=-3  \)

\((x-2)^2=-3 +4=1 \)

1.)

\(x-2=1 \)

\(x_1=3 \)       \( f(3)=-3^{3}+6 *3^{2}-9 *3=0 \)

Somit ist bei x=3 ein Extremwert (doppelte Nullstelle)

Answer 3

Klammere -x aus:

-x*(x^2-6x+9)

und erkenne die 2. binom. Formel!

abc-Formel nicht notwendig.

Comments

Warum funktioniert es nicht wenn man nur x ausklammert?

---

Es funktioniert auch dann, wenn man nur \(x\) ausklammert. Die Nullstellenform von

        \(ax^3 + bx^2 + cx\)

lautet aber nun mal nicht einfach

      \((x-x_1)(x-x_2)(x-x_3)\)

mit Nullstellen \(x_1\), \(x_2\) und \(x_3\).

Answer 4

- x^3 + 6·x^2 - 9·x
= - x·(x^2 - 6·x + 9)
= - x·(x^2 - 2·3·x + 3^2)
= - x·(x - 3)^2
= - x·(x - 3)·(x - 3)

x = 0 (einfache Nullstelle)

x = 3 (doppelte Nullstelle wegen dem Quadrat)