Aufgabe:
würde mich freuen, wenn ihr bei der 3c) und 3d) helfen könntet, damit ich diese Aufgabe abschliessen kann.
Betrachten Sie die Funktion f: R^2 --->R^2 definiert durch f(x,y) = (e^x*siny, e^x*cosy)
a) Entscheiden Sie mit Begründung, ob f injektiv ist und ob f surjektiv ist.
b) Zeigen Sie, dass die Funktion f die Bedingungen des Satzes über die Umkehrfunktion in allen Punkten von R^2 erfüllt.
c) Sei a = (0, \( \frac{pi}{2} \) und U = R x (-\( \frac{pi}{2} \) , \( \frac{pi}{2} \) eine offene Umgebung von a. Sei f|U die Einschränkung von f auf U und V = f|U das Bild von f|U. Finden Sie eine explizite Umkehrfunktion f-1 |U : V --->U und schliessen Sie daraus, dass f|U : U-->V
bijektiv ist.
d) Berechnen Sie die Jacobi-Matrizen d(f-1 |U) bei f(a) und df(a) und zeigen Sie, dass d( f-1 |U) = (df(a))-1
Problem/Ansatz:
a) f ist weder injektiv noch surjektiv ( bereits gelöst )
b) f erfüllt die Bedingungen des Satzes über die Umkehrfunktion in allen Punkten von R^2 (bereits gelöst)
c) 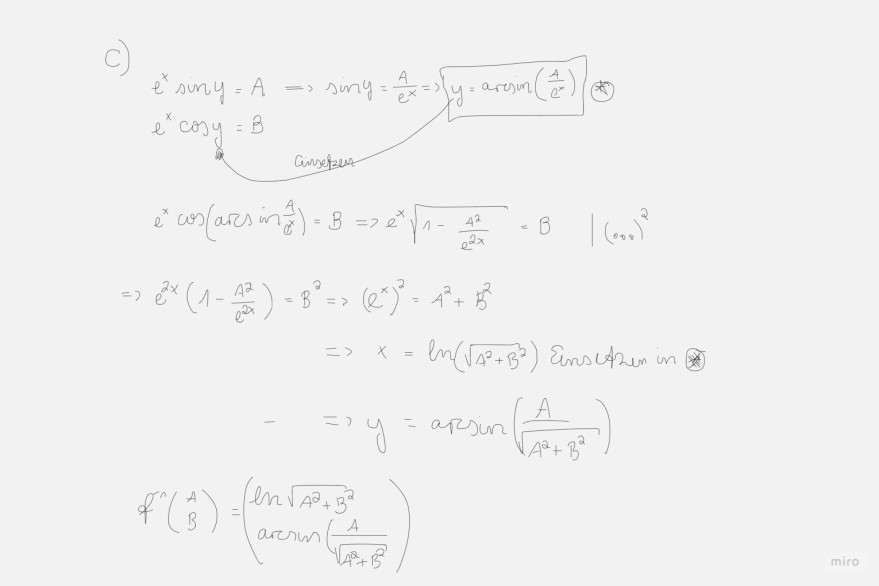
Text erkannt:
C)
\( \begin{array}{l} e^{x} \sin y=A \Rightarrow \sin y=\frac{A}{e^{x}} \Rightarrow y=\arcsin \left(\frac{A}{e^{x}}\right) \\ e^{x} \cos y=B \\ e^{x} \cos \left(\arcsin \frac{A}{e^{x}}\right)=B \Rightarrow e^{x} \sqrt{1-\frac{4^{2}}{e^{2 x}}}=B \quad \mid(0,0)^{2} \\ \Rightarrow e^{2 x}\left(1-\frac{A^{2}}{e^{2 x}}\right)=B^{2} \Rightarrow\left(e^{x}\right)^{2}=A^{2}+B^{2} \\ \Rightarrow x=\ln \left(\sqrt{A^{2}+B^{2}}\right) \operatorname{Ens} C_{\text {A }} \text { in in } \\ -\Rightarrow y=\arcsin \left(\frac{A}{\sqrt{A^{2}+B^{2}}}\right) \\ \mathscr{f}^{n}\left(\begin{array}{l} A \\ B \end{array}\right)=\left(\begin{array}{l} \ln \sqrt{A^{2}+B^{2}} \\ \arcsin \left(\frac{A}{\sqrt{A^{2}+B^{2}}}\right. \end{array}\right) \\ \end{array} \)
\( \star \)
curretser.
miro
Mit dieser Lösung von f-1 bekommt man jedoch die Gleichheit in d) nicht.
Würd mich freuen wenn wir die c) korrigieren könnten...
LG