Zur Wortbedeutung von ‚Begriff‘ schreibt Oxford Languages:
Gesamtheit wesentlicher Merkmale in einer gedanklichen Einheit; geistiger, abstrakter Gehalt von etwas.
Dieses ‚etwas’ wird in der Mathematik durch eine Zeichenkette dargestellt und oft durch stenographische Zeichen, welche an Stelle der Zeichenketten stehen sollen. Ein Beispiel:
Die Zeichenkette PROPORTIONAL hat in der Mathematik das stenographische Zeichen ~ .
Die Gesamtheit wesentlicher Merkmale dieses Zeichens kann in einer sicherlich unvollständigen Liste wiedergegeben werden (wir beschränken uns auf direkte Proportionalität):
- Zahlenpaare aus Zähler und Nenner gleichwertiger Brüche sind proportional;
- Verhältnisse entsprechender Streckenabschnitte auf zwei von einem Punkt ausgehenden Strahlen, die von zwei Parallelen herausgeschnitten werden, sind proportional;
- bei unbegrenztem Wachstum sind Bestand und Wachstumsgeschwindigkeit proportional;
- Paare (Anzahl der Stücke; Gesamtwert dieser Stücke) sind bei Stücken gleichen Wertes proportional;
- Paare entsprechender Seitenlängen in ähnlichen Figuren sind proportional;
- … … …
Hier wird deutlich, dass die meisten Begriffe im Mathematikunterricht nicht in überschaubarer Unterrichtszeit eingeführt werden können. Nicht wenige mathematische Begriffe werden über Schuljahre hinweg immer weiter vervollständigt. Um einen Begriff in einen weitergehenden Gedanken einbauen zu können und auf diese Weise Erkenntnisse zu gewinnen, muss der Begriff im Denken der/des Lernenden zu einem Superzeichen verdichtet angelegt werden. Dabei helfen die oben genannten Zeichen und insbesondere die stenographischen Zeichen. Jedes Denken braucht Zeichen, in denen sich Gedachtes verdichtet. Es gibt kein Denken ohne Zeichen. Ein Gleichheitszeichen zwischen zwei Termen kann nur angemessen in weitergehende Gedanken eingebaut werden, wenn sich mit seiner Wahrnehmung möglichst viele Regeln der Termumformung und der Gleichungslehre im Denken des/der Lernenden einstellen. Die Voraussetzung zu einer derartigen Verdichtung wird in der Semiotik ‚Hypostatische Abstraktion‘ genannt, zu Deutsch ‚vergegenständlichende Verallgemeinerung‘. Die Begriffe der Gleichheit oder der Proportionalität aus obigen Beispielen werden als Zeichen ~ oder = vergegenständlicht und behalten gleichzeitig möglichst viele Facetten ihrer wesentlichen Merkmale.
Laut Erkenntnistheorie stehen Zeichen, Objekt und Begriff in Wechselbeziehung zueinander. Dies wird in Form des sogenannten ‚epistemologischen Dreiecks‘ dargestellt:
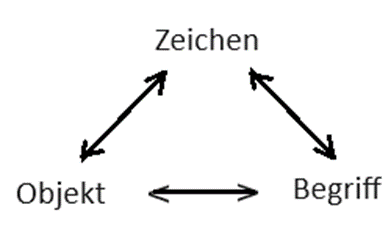
Dabei ist das Objekt dieses ‚Etwas‘ aus Oxford Languages. Das Objekt kann unmöglich getrennt werden von seinem Zeichen oder von der Gesamtheit wesentlicher Merkmale, welche sich bei der Wahrnehmung des Zeichens zu einer gedanklichen Einheit verdichten. Das Objekt selbst ist ein Abstraktum, das sich nur in seinem Begriff (oder Teilen davon) oder seinem Zeichen konkretisieren kann. Zweifel an der Existenz eines solchen nicht wirklich greifbaren Objekts würden allerdings vieles zerstören, was zum Erkenntnisgewinn gesagt werden kann. Beim Erkenntnisgewinn geht es immer um Erkenntnisse bezüglich bestimmter Objekte, die meist in Form eines Zeichens oder einer logischen Kombination von Zeichen gegeben sind. Dabei muss dieses Zeichen (diese Zeichenkette) Auslöser für einen Begriff sein. Das Ergebnis des darauf folgenden Erkenntnisgewinns wird dann das Objekt um eine zusätzliche Facette bereichern und damit den Begriff vervollständigen, welcher seinerseits als Zeichen oder Zeichenkette dargestellt werden kann. Ein Beispiel:
Das Zeichen ≡ für Restgleichheit soll vervollständigt werden, Ausgangspunkt ist die Kongruenz a≡b mod m von der nur der Begriffsanteil bekannt ist: ‚Die natürlichen Zahlen a und b haben beim Dividieren durch eine natürliche Zahl m den gleichen natürlichen Rest.‘ Durch kreatives Spiel mit diesem Begriffsanteil werden neue Begriffsanteile bezüglich des mit dem Zeichen ≡ belegten unvollständigen Begriffes gewonnen, zum Beispiel: ‚Einige Regeln der Gleichungslehre können im Kongruenzkalkül direkt übernommen werden.‘
Dieses Spiel mit mit bereits bekannten Begriffsanteilen eines Objektes mit dem Ergebnis des Gewinns neuer Begriffsanteile heißt in der Semiotik des Charles Sanders Peirce ‚Diagrammatisches Schließen‘. Dazu wurde unter Lernen nach Peirce (Semiotik) | Mathelounge einiges gesagt.