Den arithmetischen Mittenrauwert bestimmen, Integral lösen

Question

Der arithmetische Mittenrauwert \( R_{a} \) :
\( \begin{aligned} R_{\mathrm{a}} & =\frac{1}{l_{\mathrm{n}}} \cdot \int \limits_{x=0}^{l_{n}}|z(x)| \cdot d x \\ & =\frac{1}{8 \cdot \pi} \cdot \int \limits_{x=0}^{8 \cdot \pi}|0,01 \cdot \cos (x)| \cdot d x \\ & =\frac{0,00125}{\pi} \cdot \int \limits_{x=0}^{8 \cdot \pi}|\cos (x)| \cdot d x \\ & =\left.\frac{0,00125}{\pi} \cdot 4 \cdot 4 \cdot \sin (x)\right|_{0} ^{\frac{\pi}{2}} \\ & =0,0065 \mathrm{~mm} \end{aligned} \)

Guten Morgen, ich kann diese Lösung leider nicht komplett nachvollziehen.
cos integriert ist ein, 1/8pi sind 0,00125 das habe ich alles verstanden. Jedoch komme ich beim einsetzen der Grenzen nicht auf die Lösung. Ich verstehe nicht woher die 4*4 kommen und warum man dann Pi/2 nimmt.

Comments

1/8pi sind 0,00125

Das stimmt nicht. Es wurde der Faktor \(0,01\) aus dem Integral herausgezogen und es ist

$$\dfrac18\cdot 0.01 = \dfrac{1}{800}=0,00125.$$

Der Rest der Umformung besteht darin, von den 16 kongruenten Einzelflächen nur eine zu berechnen, um die Betragsklammern loszuwerden.

---

Ich verstehe nicht woher die 4*4 kommen und warum man dann π/2 nimmt.

4*4*π/2=8π

sin(π/2)=1

---

Wenn du |cos(x)| ansiehst ist die Fläche darunter periodisch in pi/2 damit sind 8pi 16 gleiche Flächen

Gruß lul

---

"Mittenrauwert":

Ich war erstaunt, mittels Google zu entdecken, dass es sowas tatsächlich gibt ....

https://www.technisches-zeichnen.net/technisches-zeichnen/diverses/rauheitswerte.php

---

Ich habe zu dem Thema nochmal eine Frage: Wenn die Funktion lautet y(x) 0,02*sin(x) und der ausgewertete Teil der Messstrecke 4pi beträgt.

Wie wäre da das Ergebnisse?

Ich denke das mein Ergebnis nicht stimmt.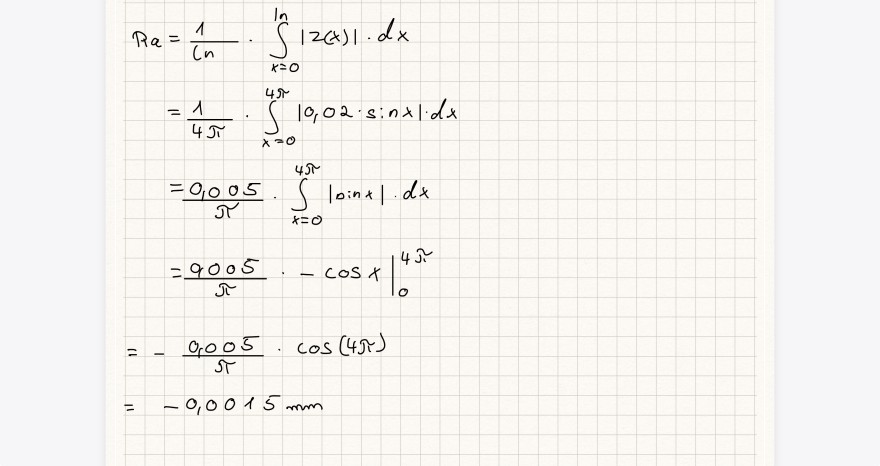

Text erkannt:

\( \begin{aligned} R_{a} & =\frac{1}{\ln } \cdot \int \limits_{x=0}^{\ln }|z(x)| \cdot d x \\ & =\frac{1}{4 \pi} \cdot \int \limits_{x=0}^{4 \pi}|0,02 \cdot \sin x| \cdot d x \\ & =\frac{0,005}{\pi} \cdot \int \limits_{x=0}^{4 \pi}|\sin x| \cdot d x \\ & =\frac{0,005}{\pi} \cdot-\left.\cos x\right|_{0} ^{4 \pi} \\ & =-\frac{0,005}{\pi} \cdot \cos (4 \pi) \\ & =-0,0015 \mathrm{~mm}\end{aligned} \)

---

Bei Deiner Nachfrage ist sowohl das 4. als auch das 5. Gleichheitszeichen falsch.

Du musst Dir überlegen, wie Du die Betragsstriche verarbeiten willst

---

Genau da komme ich leider nicht weiter.

---

Kann ich wie oben in dem Beispiel 4*4 nehmen und dann als obere Grenze Pi/4 anstatt Pi/2?

---

Nicht raten. Mach Dir ne Skizze von \(|\cos|\) auf dem gefragten Intervall, dann siehst Du sofort wie Du aufteilen und rechnen musst.

---

Ja dann müsste mein vorheriger Vorschlag stimmen, wenn ich das richtig deute.

---

Im Prinzip ja (wenn Du mit "vorheriger" die Rechnung ganz oben meinst). Aber die letzte Zahl stimmt nicht. Schon deshalb weil es bei Division durch \(\pi\) kein "glattes" Ergebnis gibt. Wenn dann, gerundet angeben, mit \(\approx\). Aber dann richtig runden.

Answer 1

Hallo

Wenn du |cos(x)| ansiehst ist die Fläche darunter periodisch in pi/2 damit sind 8pi 16 gleiche Flächen
Gruß lul

Comments

Kann mir jemand die Lösung sagen, ich habe mehrere Aufgaben zu dem Thema. Und ein Lösungsbeispiel würde mir sehr weiterhelfen?