32. Prüfen Sie, welche Lage die Gerade g relativ zum Graphen von f einnimmt.

Question

Aufgabe:

Prüfen Sie, welche Lage die Gerade g relativ zum Graphen von f einnimmt.

Problem/Ansatz:

32. Prüfen Sie, welche Lage die Gerade g relativ zum Graphen von f einnimmt.
a) f(x) = x^2- 5x, g(x) =-x - 4
b) f(x) = 2x^2 - 4x + 1, g(x) = 3x-4

c) f(x) = 3x^2 - 2x, g(x) = -2x + 3
d) f(x) = x? + 4x + 1, g(x) = 2ax, a > 0

Answer 1

z.B. bei a)    x²- 5x =-x - 4

           x²- 4x + 4 = 0

pq-Formel bringt x _1,2 =  2 ±√( 4-4)

Also nur eine Lösung   x=2 .

Graph und Gerade haben genau einen gemeinsamen Punkt.

Dort haben beide sogar die gleiche Steigung, also ist die

Gerade die Tangente an den Graphen in diesem Punkt.

Answer 2

b)

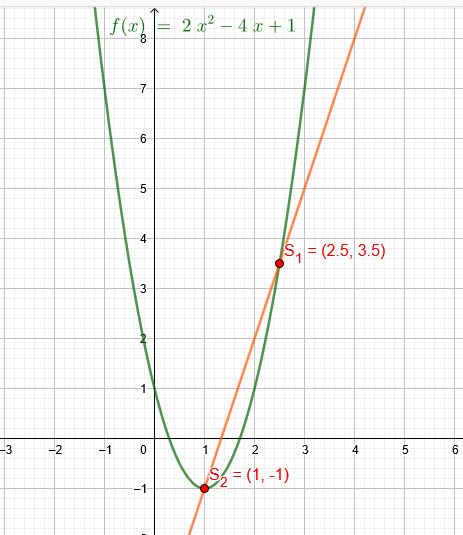
\(f(x) = 2x^2 - 4x + 1,   g(x) = 3x-4\)

\(f(x) =  g(x) \)

\( 2x^2 - 4x + 1 = 3x-4\)

\( 2x^2 - 7x = -5\)

\( x^2 - \frac{7}{2}x = -\frac{5}{2}\)

\( (x - \frac{7}{4})^2  = -\frac{5}{2}+(\frac{7}{4})^2=-\frac{40}{16}+\frac{49}{16}=\frac{9}{16}   |\sqrt{~~}\)

1.)

\( x - \frac{7}{4}  = \frac{3}{4}  \)

\( x_1   =2,5  \)

2.)

\( x - \frac{7}{4}  = -\frac{3}{4}  \)

\( x_2   =1  \)

Es existieren 2  Schnittpunkte.