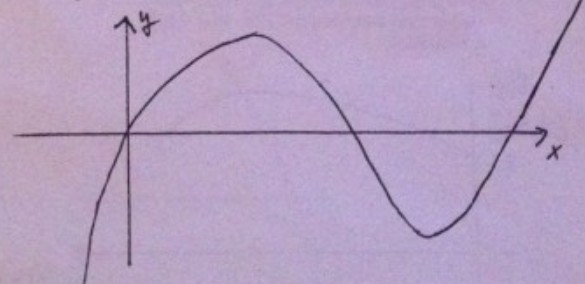
Die Funktion
\( f(x)=\frac{1}{270} \quad x^{3}-\frac{19}{9} \quad x^{2}+280 x \)
beschreibt die täglichen Zu- und Abflüsse auf den Sparkonten einer Bankfiliale, die unter dem Strich durch die Einzahlungen und Abhebungen der Kunden entstehen (x in Tagen, y in Euro).
An der Skizze des Graphen von \( f(x) \) ist zu erkennen, dass in den ersten Monaten die Kunden insgesamt mehr einzahlen als abheben und gegen Jahresende (nach dem Urlaub und vor Weihnachten) ihre Konten eher plündern als aufstocken.
Rechenbeispiel:
Am 150. Tag (30. Mal) fließen insgesamt \( f(150)=1 / 270 \cdot 150^{3}-199 \cdot 150^{2}+280 \cdot 150 \) \( =+7000 \mathrm{e} \) auf die Sparkonten der Filiale.
a) Bestimmen Sie:
- den Tag \( P \), an dem die Filiale des meiste Geld einnimmt,
- Tag den \( Q \), an dem die Filiale das meiste Geld auszahlen muss,
- den Tag \( R \) im Jahr, an dem morgens und abends dieselbe Geldsumme auf allen Sparkonten der Filiale sein müsste,
- die Geldmenge \( Z \), die die Filiale am Morgen von Tag \( Q \) bereithalten muss, um alle Abhebungswünsche erfüllen zu kännen (15 % Sicherheitsreserve).
b) Für die \( x \) -Werte (Tage) kann man aus mathematischer Sicht zwar alle möglichen Werte in die Funktionsgleichung einsetzen, aber nicht alle sind in Bezug auf die beschriebene Anwendung auch sinnvoll. Geben Sie begründet einen sinnvollen Bereich für die zulässigen \( x \) -Werte an.
c) Irgendwo in seinem Verlauf ändert der Graph von \( f(x) \) seine Krümmungsrichtung (von einer Rechtskurve in eine Linkskurve). Bestimmen Sie diesen Tag und interpretieren Sie diesen Wert hinsichtich des Verhaltens der Kunden.
d) Schätzen Sie ab, ob am Ende des Jahres \( (x=360) \) die Kunden insgesamt mehr oder weniger Geld auf ihren Sparkonten haben.