Du machst 2 Funktionen aus der Gleichung und bestimmst dann die Schnittpunkte der beiden Graphen.
x² - 9 = 0,
Erste Funktion: y = x² - 9
Hier hast du eine Parabelgleichung (Verschobene Normalparabel). Scheitelpunktform ist y = (x-0)2 - 9
Scheitelpunkt ist deshalb S(0/9)
Zweite Funktion: y=0
Geradengleichung. Steigung 0. y-Achsenabschnitt 0. Also: x-Achse
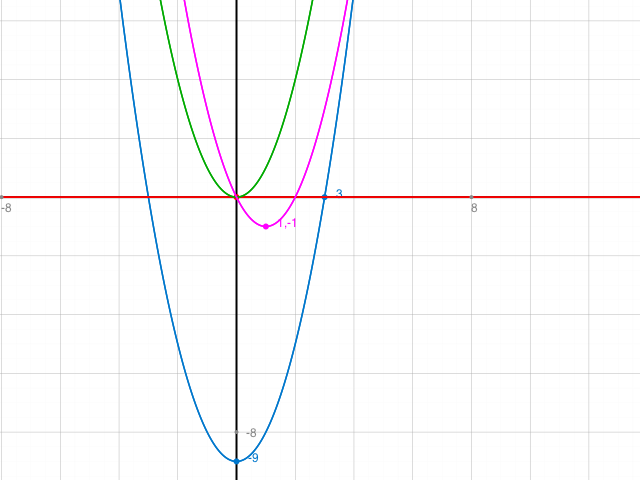
Zeichnung (für beide Beispiele). Grün: Normalparabel.
Blau: Parabel des 1. Beispiels. L= {-3,3}. Exakt, weil 3^2 =9.
Rosa: Parabel des 2. Beispiels. L= {0,2}
Beispiel 2.
x² - 2x = 0
Scheitelpunktform aus erster Funktionsgleichung machen.
1. Funktion: y = x2 - 2x |quadr. Ergänzung (Binom erzwingen mit +1 -1)
= x2 - 2x + 1 - 1
= (x-1)2 - 1
S ablesen S(1,-1)
2. Funktion y=0: x-Achse.
rosa Kurve schneidet die x-Achse exakt in x1=0 und x2=2.
rechnerische Kontrolle: x2 - 2x = x (x-2) = 0.
Produkt ist Null, wenn einer der Faktoren 0 ist. Also: x1 = 0 und x2 =2.
Alternative: zuerst die Gleichungen umformen auf
x2 = 9
und
x2 = 2x
Graphen der drei Funktionsgleichungen zeichnen.
y=x2 Normalparabel
y=9 Horizontale Gerade
y=2x Gerade durch P(0/0) mit Steigung 2
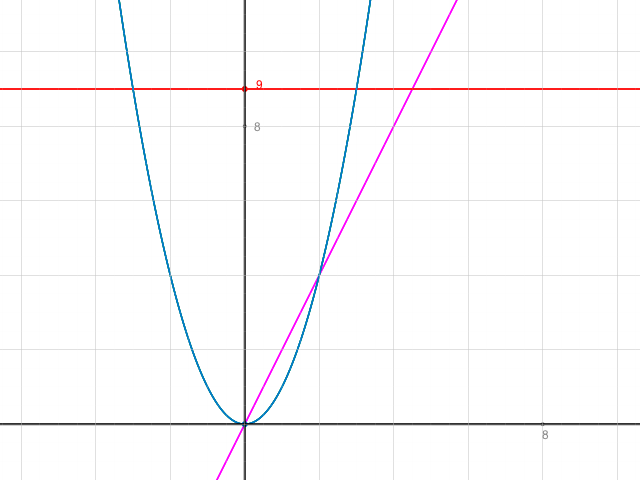
Jetzt durch die Schnittpunkte der Normalparabel mit den Geraden Parallelen zur y-Achse einzeichnen und an den Schnittpunkten mit der x-Achse die x-Werte ablesen.
Ergibt L1 = {-3, 3}
und L2 = {0,2}