Aufgabe:
Die Glaskuppel auf dem Dach eines mehrstöckigen Hauses besteht aus Glaselementen, die von Metallstreben zusammengehalten werden. Einige dieser Streben laufen von der Dachspitze strahlenförmig nach außen.
Den Bauplänen kann man die Koordinaten der Endpunkte zweier
solcher Streben entnehmen:
A (0|0|15), B (41-3| 13,5) und C (4 3 |13,5), gemessen in m.
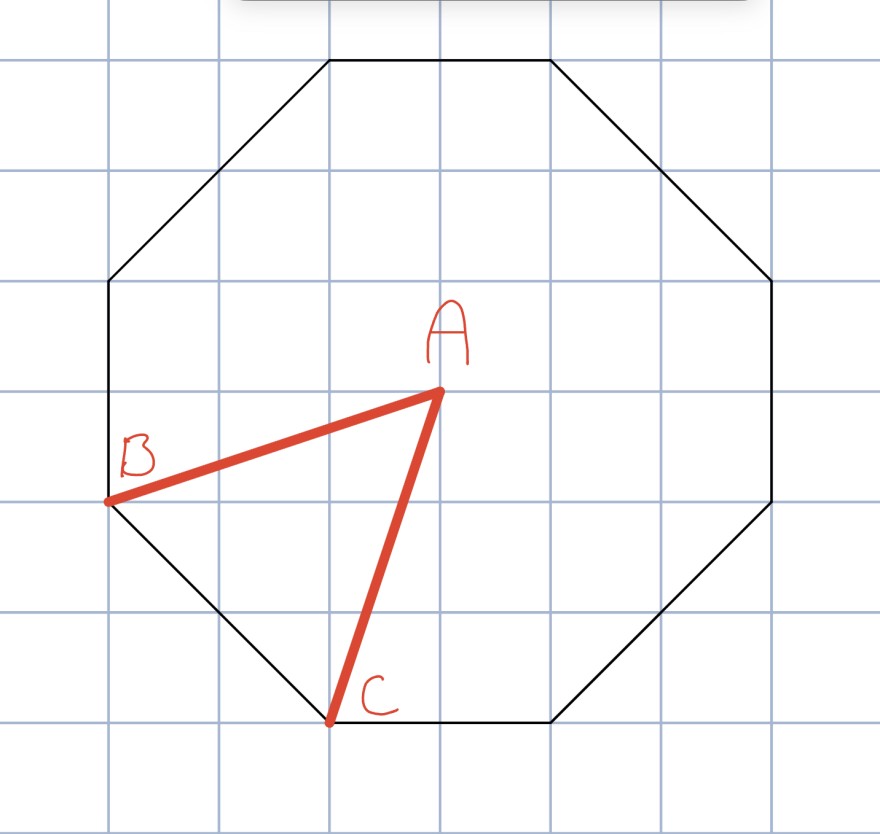
Zeigen Sie, dass die beiden Dachstreben im Bild rechts keinen rechten Winkel einschließen.
Ansatz:
Zuerst habe ich die Richtungsvektoren BA und CA gebildet. Dabei hatte ich für BA=(-4,3,1.5) und für CA=(-4,-3,1.5) heraus. Danach habe ich das Skalarprodukt berechnet:
(-4)·(-4)+3·(-3)+1,5·1,5=9,25
Dadurch habe ich heraus gefunden das es ≠ 0 ist und kein rechter Winkel vorhanden ist.
Habe ich richtig gerechnet?
Beste Grüsse Milan