(M∪N)\L = M∪(N\L) ⇔ M∩L={} beweisen

Question

Hallo Freunde der Mathematik,

ich sitze gerade an einer Problemstellung der Mengenlehre. Ich verstehe das Problem und habe es mir mit Hilfe von Venn-Diagrammen schon veranschaulicht, ja sogar "bewiesen", allerdings scheitere ich am formalen, mathematisch korrekten Beweis.

Aufgabe:

Seien L, M, N Mengen. Zeigen Sie

(M∪N)\L ⊂ M∪(N\L)

und dass

(M∪N)\L ⊃ M∪(N\L)

genau dann wenn,

M∩L={}

Problem/Ansatz:

Ich weiß, dass das bedeutet, dass die ersten 2 "Gleichungen" gleich sind (da sie ja Teilmengen von einander sind) und dass das wiederum äquivalent sein soll zum letzten Ausdruck (wie im Titel). Aber was ist hier der Ansatz, ich denke mal kein direkter Beweis? Ein Widerspruchsbeweis vielleicht?

Hier ist einer meiner Ansätze..

(M∪N)\L = M∪(N\L) 

⇔ (x∈M oder x∈N) und x∉L = x∈M oder (x∈N und x∉L)

⇔ (x∈M und x∉L) oder (x∈N und x∉L) = (x∈M oder x∈N) und (x∈M oder x∉L)

Ein (richtiger) Ansatz würde mir wirklich schon reichen, da ich mir gerne selber die Lösung erarbeiten würde.

Ich danke euch schon mal herzlich für eure Zeit und Bemühungen.

Edit: hier noch meine Venn-Diagramme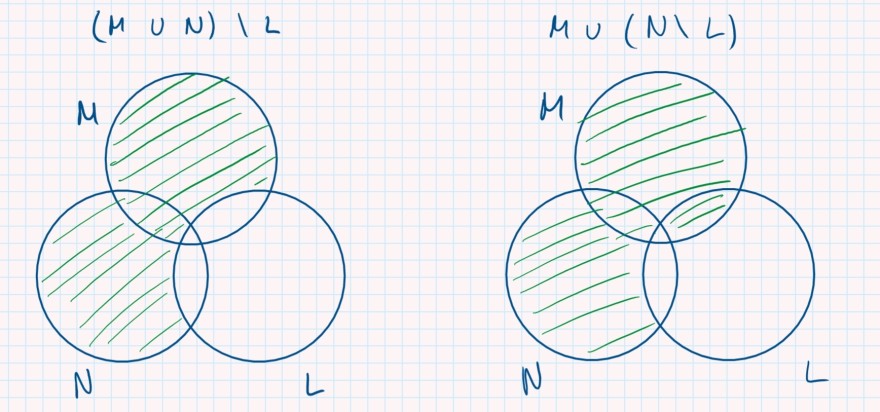

Text erkannt:

\( (M \cup N) \backslash L \)
\( M \cup(N \backslash L) \)

Answer 1

Genau dann, wenn man von der Vereinigung zweier disjunkter Mengen M und N eine Menge L wegnimmt, die mit M kein Element gemeinsam hat, genügt es L von N wegzunehmen.

Comments

ok.. was wäre dann mein ansatz für den formalen beweis?

---

Wegen der Äquivalenz sind zwei Beweise zu führen. Dabei muss man sich auf die Elemente der Mengen beziehen:

1. ((x∈M∨x∈N)∧¬x∈L) ∧ x∈M∨(x∈N∨¬x∈L) ⇒ ((x∈M∧x∈L)∧x∈∅)

2. ((x∈M∧x∈L)∧x∈∅) ⇒  ((x∈M∨x∈N)∧¬x∈L) ∧ x∈M∨(x∈N∨¬x∈L)