Differenzialrechnung bei ganzrationalen Funktionen.

Question

Aufgabe:

Fertige Sie eine Skizze des Funktionsgraphen an. Stellen Sie die Funktionsgleichgng auf. Prüfen Sie anschließend mit einem digitalen Hilfsmittel, ob der Graph der ermittelten Funktion bzw. die Funktion selbst tatsächlich die gegebenen Merkmale hat.

-> Der Graph einer quadratischen Funktion schneidet die y-Achse bei 5 und hat im Punkt P(1|2) die Steigung -4.

Problem/Ansatz:

Ich verstehe überhaupt nicht, wie ich die Aufgabe lösen soll. Würde mich über Antworten sehr freuen!!

Answer 1

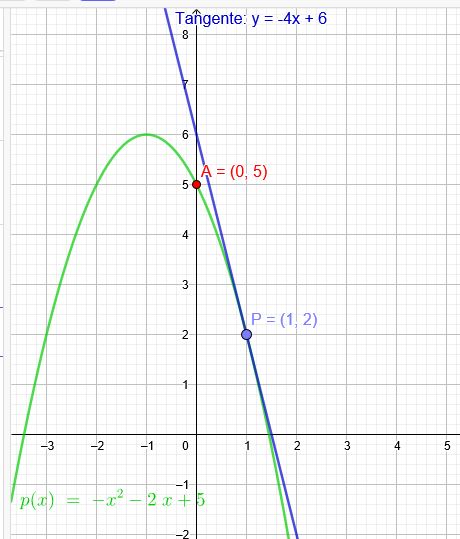
Der Graph einer quadratischen Funktion schneidet die y-Achse bei 5 und hat im Punkt P(1|2) die Steigung -4.

Ich verschiebe um 5 Einheiten nach unten : schneidet die y-Achse bei 0

\(f(x)=a*x*(x-N)=a*[x^2-x*N]\)

\(P(1|2)→P´(1|-3)\)

\(f(1)=a*[1-N]\) 

\(a*[1-N]=-3\)  →  \(a=\frac{3}{N-1}\)

\(f(x)=\frac{3}{N-1}*[x^2-x*N]\)

\(f´(x)=\frac{3}{N-1}*[2x-N]\)

\(f´(1)=\frac{3}{N-1}*[2*1-N]\)

\(\frac{3}{N-1}*[2-N]=-4\) →\(\frac{3}{N-1}*[N-2]=4\)  

\(N=-2\)     \(a=\frac{3}{-2-1}\)  →\(a=-1\)

\(f(x)=-[x^2+2x]=-x^2-2x\)

5 Einheiten nach oben:

 \(p(x)=-x^2-2x+5\)

Answer 2

f(x) = ax^2+bx+c

f '(x)= 2ax+b

f(0) = 5

f(1) = 2

f '(1) = -4

c= 5

a+b+5= 2

b= -3-a

2a+b= -4

2a+-3-a = -4

a= -1

b= -2

f(x) = -x^2-2x+5

Comments

Mach doch mal die Probe mit dem von Dir berechneten f

---

Danke.

Ich hatte mit c= 0 statt c= 5 gerechnet.

---

@ggT
Deine Antwort ist hier eindeutig die bessere und offensichtlich einfachere Lösung. Außerdem ist sie meines Erachtens im Sinne des Fragestellers auch geeigneter.