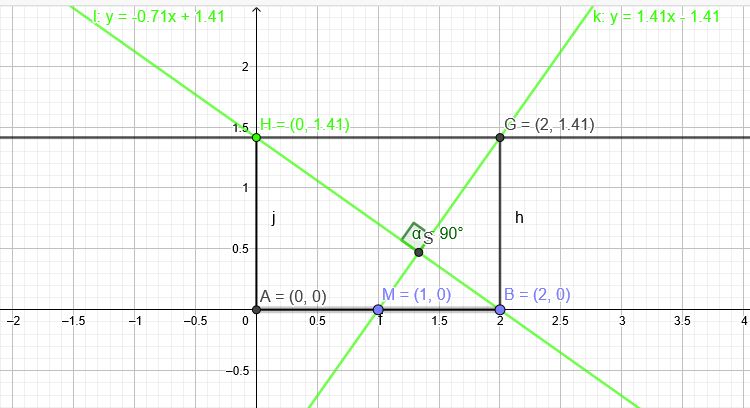
Ebene \(ABGH\) ins \(x,y\) Koordinatensystem legen.
Länge der Diagonalen von B nach G mit \(x=1\): \( \sqrt{2} \)
Geradengleichung \(BH\):
\( \frac{x}{2} +\frac{y}{\sqrt{2}}=1\)
\( y=-\frac{1}{2}\cdot\sqrt{2}\cdot x+\sqrt{2}\) → \(m_1=-\frac{1}{2}\cdot\sqrt{2}\)
Geradengleichung \(GM\):
\( \frac{y-0}{x-1}=\frac{\sqrt{2}-0}{2-1}\)
\( \frac{y}{x-1}=\frac{\sqrt{2}}{1}\)
\( y=\sqrt{2} \cdot x-\sqrt{2}\) → \(m_2=\sqrt{2}\)
\(m_1 \cdot m_2=-1\)
Somit ist der Winkel \(90°\)