Wie Winkel zwischen zwei Raumdiagonalen in einem Quader berechnen?

Question

Ich habe einen Quader mit folgenden Seitenkanten gegeben:

a = 25,5cm

b = 12,6cm

c = 17,7cm

Wie kann ich jetzt mit den trigonometrischen Winkelfunktionen den Winkel zwischen zwei Raumdiagonalen berechnen?

Answer 1

Das sage ich dir, wenn du die Länge der Raumdiagonale berechnet hast.

Comments

Die Länge der Raumdiagonale beträgt etwa 33,5 cm.

---

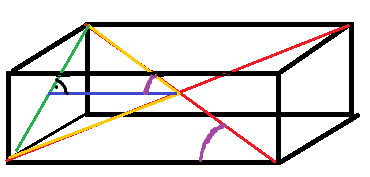
Die Hälfte deines gesuchten Winkels (violett) findest du in dem eingezeichneten rechtwinkligen Dreieck mit den Kanten

halbe Raumdiagonale (orange)

halbe Kantenlänge (blau)

halbe Flächendiagonale (grün).

Ein Winkel der gleichen Größe tritt auch in dem ähnlichen Dreieck

mit jeweils doppelt so großen Kantenlängen auf.

Answer 2

Quader mit folgenden Seitenkanten gegeben: x= 25,5; y= 12,6; z= 17,7.

Die Raumdiagonalen haben die Vektoren \( \vec{u} \) = \( \begin{pmatrix} x\\y\\z \end{pmatrix} \) und \( \vec{v} \) =\( \begin{pmatrix} -x\\y\\z \end{pmatrix} \) .

Dies einsetzen in: cos(α)= \( \frac{\vec{u}·\vec{v}}{|\vec{u}|·|\vec{v}|} \) .