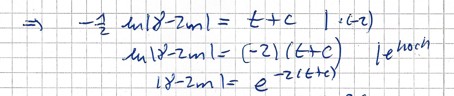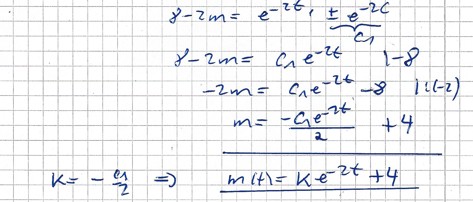Differenzialgleichung in der Technik

Question

Aufgabe:

Text erkannt:

Bei einer bestimmten chemischen Reaktion ändern sich die vorhandenen Massen der beteiligten Stoffe mit der Zeit. Für einen dieser Stoffe kann die vorhandene Masse näherungsweise durch die Differenzialgleichung \( \frac{\mathrm{d} m}{\mathrm{~d} t}=8-2 \cdot m \) beschrieben werden.
\( t \)... Zeit in \( \mathrm{s} \)
\( m(t) \)... Masse dieses Stoffes zur Zeit \( t \) in mg
Eine Lösung dieser Differenzialgleichung wurde unter Verwendung einer Anfangsbedingung ermittelt.
- Ordnen Sie den beiden Aussagen korrekt zu. [2 zu 4]
\begin{tabular}{|l|l|}
\hline \begin{tabular}{l}
Für \( t \rightarrow \infty \) nähert sich \\
der Graph der Lösung des \\
homogenen Teils dieser \\
Differenzialgleichung...
\end{tabular} & \\
\hline \begin{tabular}{l}
Für \( t \rightarrow \infty \) nähert sich der \\
Graph der Lösung dieser \\
Differenzialgleichung...
\end{tabular} & \\
\hline
\end{tabular}
\begin{tabular}{|c|c|}
\hline A & ... asymptotisch der \( t \)-Achse. \\
\hline B & \begin{tabular}{l}
... asymptotisch der waagrechten \\
Gerade mit Ordinatenabschnitt 8.
\end{tabular} \\
\hline C & \begin{tabular}{l}
... asymptotisch der waagrechten \\
Gerade mit Ordinatenabschnitt 4.
\end{tabular} \\
\hline \( \mathrm{D} \) & \begin{tabular}{l}
... asymptotisch der waagrechten \\
Gerade mit Ordinatenabschnitt -2 .
\end{tabular} \\
\hline
\end{tabular}

Problem/Ansatz:

würde gerne wissen wie man auf diese Funktion kommt um die Lösung von der 2 Frage zu haben

Text erkannt:

\( m(t)=4-m_{0} * e^{-2 * t} \)

Answer 1

Hallo,

Es sollte noch Anfangsbedingung in der Aufgabe angegeben sein?

Für k= - m₀ kommt man auf die angegebene Lösung.   

Für \( t \rightarrow \infty \) nähert sich der Graph der Lösung des homogenen Teils dieser Differenzialgleichung -->Lösung A

Für \( t \rightarrow \infty \) nähert sich der Graph der Lösung dieser Differenzialgleichung

-------->Lösung C

Lösung via Trennung der Variablen: