Hallo Freunde. Folgende Frage.
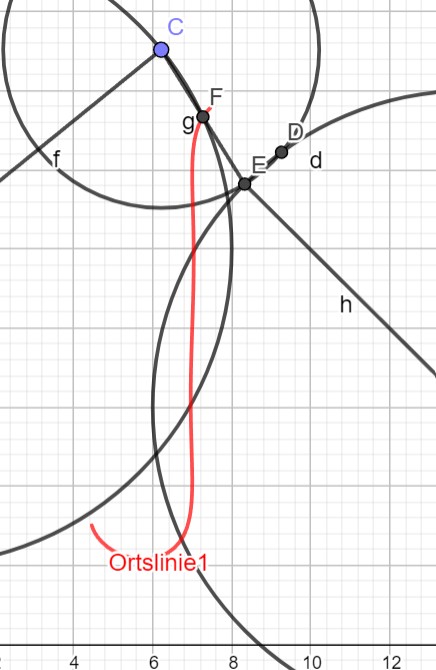
Hat die Watt'sche Kurve eine genaue gerade Strecke in ihrer Mitte? Falls ja wäre eine Begründung fein. Ich komme leider nicht drauf.
Eben jene:
Geometrisch.
Algebraisch:
960400-505680 y+120852 y^(2)-14768 y^(3)+1077 y^(4)-48 y^(5)+y^(6)-329280 x+128912 y x-19572 y^(2) x+1456 y^(3) x-42 y^(4) x+58212 x^(2)-18768 y x^(2)+1794 y^(2) x^(2)-96 y^(3) x^(2)+3 y^(4) x^(2)-7252 x^(3)+1456 y x^(3)-84 y^(2) x^(3)+717 x^(4)-48 y x^(4)+3 y^(2) x^(4)-42 x^(5)+x^(6)=0