Finden Sie einen nicht vollständigen Maßraum (X, \mathcal{A}, \mu) für X=\{1,2,3\} und bestimmen Sie die …

Question

Aufgabe:

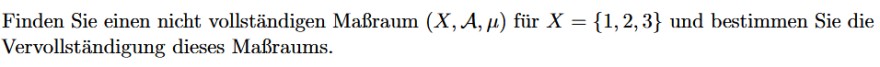
Text erkannt:

Finden Sie einen nicht vollständigen Maßraum \( (X, \mathcal{A}, \mu) \) für \( X=\{1,2,3\} \) und bestimmen Sie die Vervollständigung dieses Maßraums.

Problem/Ansatz:

Bekomme leider kein beispiel hin. Wäre dankbar für hilfe

A={leere Menge, {1,2,3},{1},{2},{3},{1,2},{1,3},{2,3}} aber mehr finde ich nicht

Comments

Vollständig heißt ja , dass Teilmengen von Nullmengen wieder Nullmengen sind. Also muss ich ein Maß konstruieren bei dem das schief geht. Aber wie komme ich an so ein Maß

---

wie komme ich an so ein Maß

Verkleinere deine Menge A

---

Und dann?

A={leere Menge, {1,2,3}, {1},{2,3}}

---

Dann fängst du an, den Elementen dieser (jetzt brauchbaren) Menge A Maße zuzuordnen.

---

Ok aber wie macht man das geschickt? Verstehe nicht Ganz wie ich die Maße wählen muss damit es hinhaut

---

Müsste ich eventuell {1,2,3} =0 und {1,2}=1

Dann {1}=0 und {}=0

---

Du musst ein bisschen herumprobieren. Sehr viele Möglichkeiten gibt es ja bei vier Mengen in A nicht. Es klappt mit µ({1})=1 und µ(X)=1.

Ergänzung nach Überschneidung: Überlege dir, warum µ({1,2})=1 und µ(X)=0 nicht gleichzeitig funktionieren können.

---

Moment. Jetzt Blicke ich nicht ganz was {2,3} und {} haben. :D

Weil das dann glaube ich kein Maß wäre

---

was {2,3} und {} haben  Das kann man dann ausrechnen.

Weil das dann glaube ich kein Maß wäre Warum nicht ?

---

Wäre dann {2,3} =1 und {} = 0?

Dann wäre die Summe 1 und die Vereinigung 0

---

Leider bist du jetzt offenbar nur noch am Raten anstatt die Definition eines Maßraumes zu benutzen, wohl in der Hoffnung, dass ich dir irgendwann die ganze Aufgabe gelöst haben werde. Das ist nicht meine Art.

---

Ich würde es gerne besser beantworten aber ich Blicke es leider nicht wirklich.

Nochmal zu der Aufgabe.

Also eine Nullmenge hat das Maß 0.

Und vollständig wie oben beschrieben . Wenn jetzt {1} {X} das Maß eins haben und damit es ein Maß ist muss die leere Menge das Maß 0 haben.

Jetzt ist mir nicht ganz klar was {2,3} ist. Nach der Definrion von Vollständigkeit von muss es doch so sein dass das Maß einer Menge 0 ist und die Teilmenge davon das Maß 1 hat damit die Vollständigkeit zerbricht.

---

Also eine Nullmenge hat das Maß 0. Das ist die Definition des Begriffs "Nullmenge". Die leere Menge ist immer eine Nullmenge.

Jetzt ist mir nicht ganz klar was {2,3} ist Benutze die σ-Additivität für die Mengen {1} und {2,3}.

Nach der Definrion von Vollständigkeit von muss es doch so sein dass das Maß einer Menge 0 ist und die Teilmenge davon das Maß 1 hat Nein, es kann auch sein, dass eine Teilmenge einer Nullmenge gar kein Maß hat, aber genau das kann bei vst. Maßräumen nicht passieren.

---

{2,3} muss 0 sein denn die Vereinigung ist X selber und das war 1. Und die Summe der einzelnen Maße muss 1 sein da aber {1} schon 1 ist muss {2,3} 0 sein oder gar kein Maß haben

---

muss {2,3} 0 sein ok   oder gar kein Maß haben falsch, da Element von A.

Die Beantwortung weiterer Fragen müsste bis morgen jemand anders übernehmen.

---

Ok danke dir

---

Wäre das dann die vervollständigung?

A^={leere Menge, X, {1},{2},{3},{2,3}}