Aufgabe:
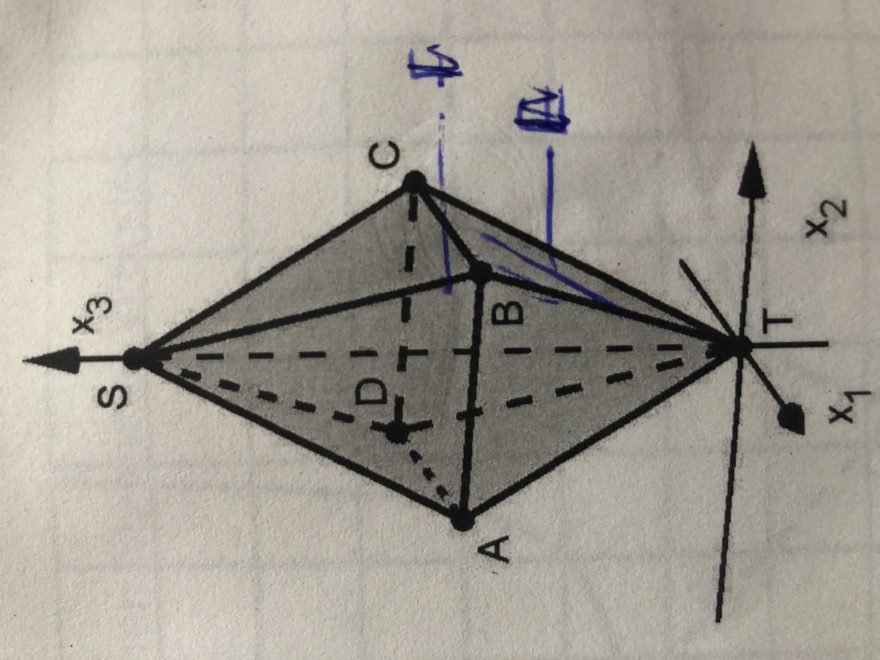
Alle Ebenen der Schar schneiden sich in einer Gerade. Weisen Sie nach, dass die Kante BC der Pyramide (siehe Abbildung) auf dieser Gerade liegt.
Die Gleichung der Ebene, die von den Punkten BC und T aufgespannt wird lautet :
F: 12 x2 - 5 x3 =0
E(k): kx2-5x3=5k-60 mir k e R
B(5|5|12) C(-5|5|12)
Problem/Ansatz
Ich habe die versucht die Schnittgerade auszurechnen, indem ich mir zwei allgemeine Ebenengleichungen für k und m mit k≠m notiert habe und durch Subtraktion eine vom Parameter unabhängige Gleichung ermittelt habe, in der g liegt. Mit dieser Gleichung kann dann eine Gleichung für g gewinnen werden -das war meine Idee und jetzt zur Umsetzung :
kx2 -5x3 = 5k -60
mx2-5x3 = 5m -60
————————- (Subtraktion)
(m-k)x2 = 5(k-m) | :(k-m)
x2= 5
Wenn man es in E(k) einsetzt kommt :
5k-5x3=5k-60 | -5k |:5
x3 = 12
Daraus kann ich keine Gerade bilden .
Viel komischer finde ich die Lösung, sie lautet einfach nur : „für B und C gilt k*5-5*12=5k-60”
Was wurde da gemacht. Danke im Voraus ihr seid die Besten