bestimmen, ob Verteilfunktion

Question

Aufgabe:

Hallo, ich habe eine Frage. ich verstehe nicht ganz, wie man folgendes Problem lösen kann. Ich habe zwar die lösungen, aber ich kann es nicht nachvollziehen.

Ich soll bestimmmen, welche der folgenden Aufgaben verteilfunktionen sind

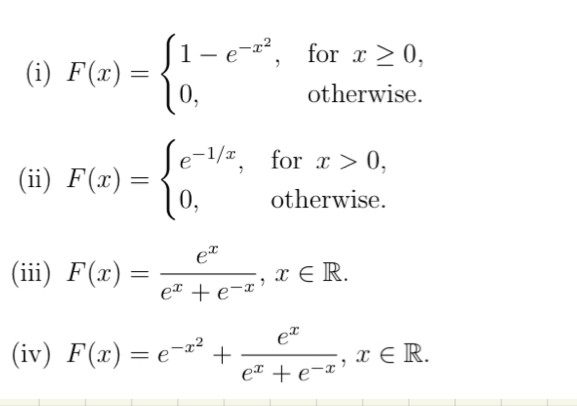
Text erkannt:

(i) \( F(x)=\left\{\begin{array}{ll}1-e^{-x^{2}}, & \text { for } x \geq 0, \\ 0, & \text { otherwise. }\end{array}\right. \)
(ii) \( F(x)=\left\{\begin{array}{ll}e^{-1 / x}, & \text { for } x>0, \\ 0, & \text { otherwise. }\end{array}\right. \)
(iii) \( F(x)=\frac{e^{x}}{e^{x}+e^{-x}}, x \in \mathbb{R} \).
(iv) \( F(x)=e^{-x^{2}}+\frac{e^{x}}{e^{x}+e^{-x}}, x \in \mathbb{R} \).

Problem/Ansatz:

Man müsste die drei properties ( rechtsstetig, aufsteigend, grenzwerte 1 und 0 ) prüfen, aber ich bin mir nicht sicher, wie ich das bei diesen Funktoinen genau machen muss und ob ich die Ableitung zur berechnung verwenden muss oder nicht...

Answer 1

Du könntest die Ableitung benutzen um zu untersuchen, ob eine Funktion monoton steigend ist.

Ansonsten hilft natürlich auch sich die Funktionen mal zu skizzieren bzw. skizzieren zu lassen.

~plot~ (1-e^(-x^2))*(x>0);(e^(-1/x))*(x>0);e^x/(e^x+e^(-x));e^(-x^2)+e^x/(e^x+e^(-x)) ~plot~

Ansonsten sag doch mal konkret wo das Problem bei der Grenzwertberechnung oder der Überprüfung der rechtsseitigen Stetigkeit liegen.

Comments

Vielen Dank für deine Antwort. Wenn der plot da ist, ist es kein grosses problem mehr, das festzustellen, ich habe aber mühe, diese Funkitonen im Kopf zu plotten.. hast du da tipps ?

---

Die ersten beiden sollten für dich kein Problem darstellen. Die letzten beiden ist schon schwieriger aber dort könnte eine Wertetabelle auch beim Skizzieren helfen.

Wenn du weißt das die Funktion im betrachteten Intervall monoton steigend ist, sollte das nicht so wild sein mit der Wertetabelle.