Hallo eine Grundsatzfrage zum Gauß-Algorithmus.
Kann ich auch so wie in rot dargestellt vorgehen? Also Zeile 2 mit Zeile 3 und umgekehrt gleichzeitig verrechnen?
Das Ergebnis weicht zu meiner anderen Lösung in Schwarz ab.
Danke und Vg
Don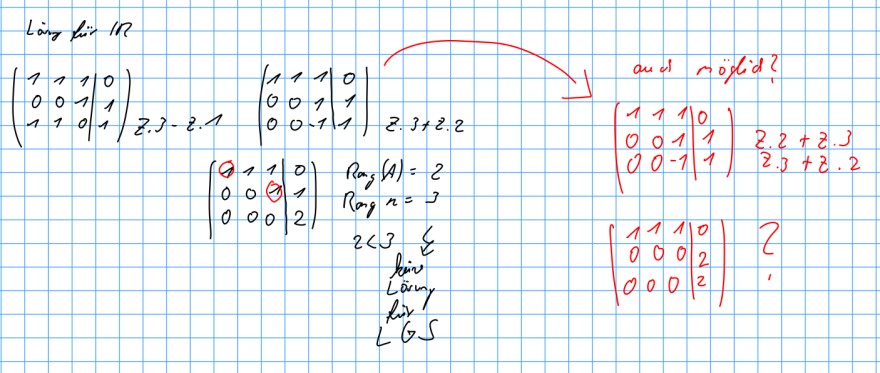
Text erkannt:
\( \begin{array}{l}\text { Laing hirs In } \\ \left(\begin{array}{lll|l}1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1\end{array}\right)_{z \cdot 3 \cdot z \cdot 1}^{z \cdot 1}\left(\begin{array}{ccc|c}1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & -1 & 1\end{array}\right) z \cdot 3+z \cdot 2 \\ \left(\begin{array}{lll|l}0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 2\end{array}\right) \quad \begin{array}{r}\text { Rang }(A)=2 \\ \text { Rang } n=3\end{array} \\ \begin{array}{l}2<3 \text { E } \\ \text { hin } \\ \text { Loing } \\ \text { hiv } \\ \text { Lis }\end{array} \\ \text { and nöglid? } \\ \left(\begin{array}{ccc|c}1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & -1 & 1\end{array}\right) \quad \begin{array}{l}z \cdot 2+z \cdot 3 \\ z \cdot 3+z \cdot 2\end{array} \\ \left(\begin{array}{lll|l}1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 2\end{array}\right) \quad 2 \\\end{array} \)