Bestimme die Gleichung der Parallelen zur Geraden g : y = x + 7, welche Graph y = x^2

Question

Aufgabe:

Bestimme die Gleichung der Parallelen zur Geraden g : y = x + 7, welche Graph y = x²
a. berührt, b. senkrecht schneidet.

Problem/Ansatz:

Man weiss ja durch y= mx+q, dass m = 1 ist. Woraus man wiederum herausfindet das x = 0.5 ist. Wie weiss ich wann, bzw. wo sich diese jetzt schneiden und von wo weiss ich wo die Senrechte schneidet?

Answer 1

Hallo

a) du kannst schon differenzieren, dann stelle fest wo x^2 die Steigung 1 hat

b) kein a) alle Parallelen haben die Form y=x+a schneide diese Gerade (gleichsetzen) mit x^2

du hast eine quadratische Gleichung, ist die Diskriminante 0 hat man nur einen Punkt, also Tangente

c)senkrecht zu x+7 ist jede gerade mit der Steigung -1 , dann wie a oder b

Gruß lul

Comments

Hier eine Skizze zur Kontrolle

~plot~ x^2;x-0.25;x+0.75;{0.5|0.25};{-0.5|0.25} ~plot~

---

schade, der Frager muss nichts mehr tun

lul

---

Wie kommst du darauf das er nichts mehr tun muss, nur weil er einen Funktionsterm zur Kontrolle hat? Es geht doch darum den Funktionsterm zu erhalten und nicht nur abzuschreiben.

---

Du kennst SuS anscheinend schlecht, die HA ist mit Abschreiben gelöst! nur in der Klassenarbeit braucht man die Rechnung

lul

Answer 2

berühren:

f(x) =g(x)

f '(x) = g'(x)

a) x+7 = x^2

b) 1= 2x

senkrecht schneiden:

x+7= x^2

f '(x)*g'(x) = -1

Answer 3

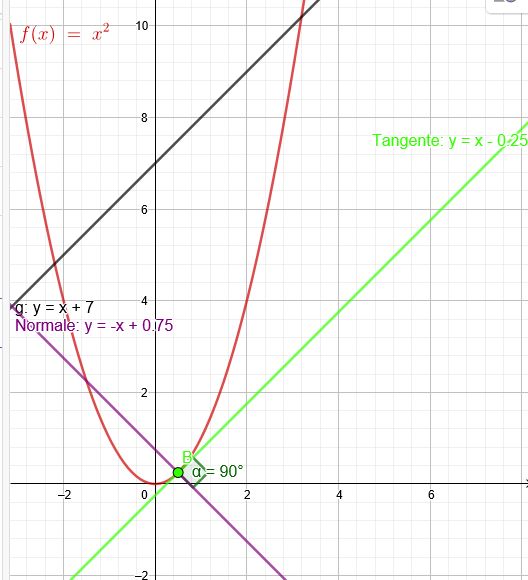
Bestimme die Gleichung der Parallelen zur Geraden  \(  g : y = x + 7\), welche Graph \(y = x^2\)
a. berührt:

\(x^2=\blue{1}x+7\)

\(x^2-1x=7\)

\((x-\red{0,5})^2=7+0,5^2\)

Die Berührstelle der Tangente ist \(x=\red{0,5}\)     \(y(\red{0,5}) = 0,25\)

Tangentengleichung:   Punkt- Steigungsform der Geraden:

\( \frac{y-0,25}{x-0,5}=\blue{1}\)

\( y=x-0,25\)

b. senkrecht schneidet:

\( \frac{y-0,25}{x-0,5}=-1\)

\( y=-x+0,75\)