Aufgabe:
Sei T eine exponentialverteilte Zufallsvariable mit Rate 1. Weiter sei X eine kontinuierliche Zufallsvariable, welche bedingt
auf T=t die Dichte 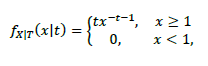 hat.
hat.
1. Gib die gemeinsame Wahrscheinlichkeitsdichte von X und T an.
2. Berechne die marginale Wahrscheinlichkeitsdichte von X.
3. Berechne die Wahrscheinlichkeitsdichte von T bedingt auf X=1 und bestimme damit den Erwartungswert von T bedingt auf X=1.
Text erkannt:
\( f_{X \mid T}(x \mid t)=\left\{\begin{array}{cc}t x^{-t-1}, & x \geq 1 \\ 0, & x<1\end{array}\right. \)
Problem/Ansatz:
Leider habe ich keinen Ansatz, da ich bisher keine Aufgabe dieser Art bearbeitet habe. Ich hab versucht durch anderen Aufgaben dieser Art einen Lösungsansatz zu finden, in älteren Aufgabenstellungen wurden "exponentialverteilt" und "kontinuierlich" in diesem Zusammenhang jedoch nie definiert. Welche Rolle spielen die Definitionen in diesem Zusammenhang? Ich wäre sehr dankbar für Lösungsansätze / Hilfestellungen zu den drei Aufgaben.