Aufgabe:
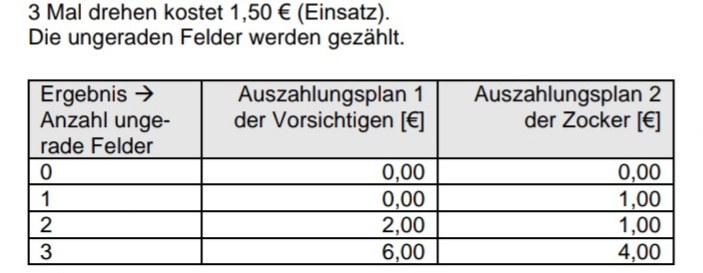
Es geht um ein Glücksrad dass 3 Mal gedreht wird und Einsatz 1,50 € kostet. Die ungeraden Felder werden gezählt.
Berechne P(X=xi) mit dem Auszahlplan der Vorsichtigen für xi 0,50 und 4,50 € bzw. das 2 und 3 orange Feld und berechne deren Erwartungswert. Ist das Spiel nun fair oder nicht?
Problem/Ansatz:
Für P(X=xi) und den Erwartungswert habe ich für 1,2 hinbekommen aber wie rechne ich das mit 2 und 3