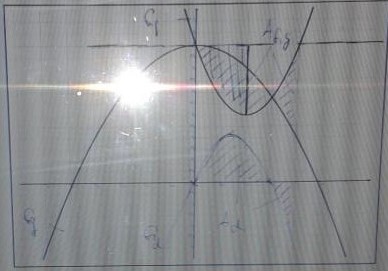
1.2.1 Die beiden Graphen Gf und Gg schließen im Intervall [0; 2] eine Fläche ein. Schraffieren Sie diese im KS. Berechnen Sie die Schnittstellen von f und g
1.2.2 Geben Sie die beiden Differenzfunktionen an. Skizzieren Sie eine davon in das KS und schraffieren Sie die Fläche, die die gleiche Maßzahl hat, wie die in 1.2.1 angegebene. Berechnen Sie diesen Flächeninhalt.
Lösungen:
1.2.1 Schnittstellen: \( 3 x^{2}-6 x+6=6-x^{2} \Leftrightarrow \ldots \Leftrightarrow x=0 \vee x=\frac{3}{2} \)
1.2.2
\( d_{1}(x)=4 x^{2}-6 x \quad \Rightarrow d_{2}(x)=-d_{1}(x)=-4 x^{2}+6 x \)
\( G_{4} \qquad d_{1}\left(\frac{3}{4}\right)=2 \frac{1}{4} \) ist \( y- \)Koordinate des Scheitelpunkts
Flächenberechnung:
\( \mathrm{A}=\int\left( -4 \mathrm{x}^{3}+6 x \right) \mathrm{~d} \mathrm{x}+ \left| \int \limits_{\int}^{2}\left(-4 \mathrm{x}^{3}-6 x\right) \mathrm{d}x \right| =\frac{9}{4}+\frac{11}{12}=3 \frac{1}{6} \)