Wie vereinfache ich einen Ausdruck mit Logarithmus im Exponenten bei ungleicher Basis?

Question

Aufgabe: 34) 9 ^log₃ ²⁰

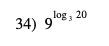
Text erkannt:

34) $9^{\log _{3} 20}$

Problem/Ansatz:

Wie vereinfache ich diesen Ausdruck?

Dadurch, dass 9 und log₃ nicht inversis sind, müsste ich wahrscheinlich eine Logarithmus-Regel anwenden, um sie inversis zu machen, richtig? Aber welche?

Die Lösung ist 400

Answer 1

$= (3^2)^{log_3(20)} = 3^{2\cdot log_3(20)} = 3^{log_3(20^2)} = 20^2 = 400$

Comments

Vielen Dank!!!

Answer 2

$9 = 3^2$ und dann Potenzgesetze anwenden.

Answer 3

$9^{\log _{3} 20}$ = $3^{2·log_3 20}$ = $3^{log_3 400}$ = 400.