Hallo,
\( \begin{array}{l}L\{f(t)\}=F(s)=\int \limits_{0}^{\infty} f(t) \cdot e^{-s t} d t \\ f(t)=42 e^{-t} \cdot \sin (17 t)\end{array} \)
->zusammenfassen und 2 mal partiell integrieren.
Hinweis: Du kannst auch die 42 erstmal unberücksichtigt lassen , weil konstanter Faktor vor das Integral geschrieben werden kann und zum Schluß dann berücksichtigen.

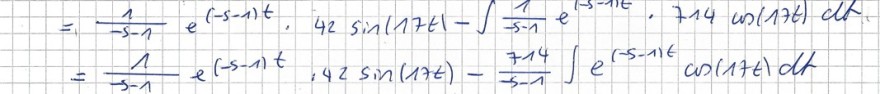
dann ein 2.Mal partiell integrieren und die Grenzen einsetzen
Ergebnis :
F(s) =\( \frac{714}{(s+1)^{2}+289} \)