Aufgabe zu Ober- und Untersumme

Question

Aufgabe:

Gegeben ist der Graph einer Funktion g mit g(x) = - 2x²+ 8. Berechne näherungsweise den Flächeninhalt, welchen der Graph von g mit der x-Achse im Intervall [0; 4] einschließt mit Hilfe von Ober- und Untersummen. Unterteile das Intervall dazu in n gleich große Teilintervalle. Zeichne die dazugehörigen Rechtecke in die Abbildungen ein (Ober- und Untersummen).

a) n=2, b=n=4, c=8
Problem/Ansatz:

Ich versteh keine der Aufgaben, denn wir haben Lösungen bekommen und meine Lösungen stimmen nicht überein. Zum Beispiel bei a hab ich eine Wertetabelle angelegt:  0= 8 ; 2=0 ; 4=-24. meine Lösung für die Untersumme wäre 2x(8+0) =16 und für die Obersumme 2x(0-24) =-48. die Lösung, die wir bekommen haben, besagt, dass die Obersumme 25 ergibt und die Untersumme 0.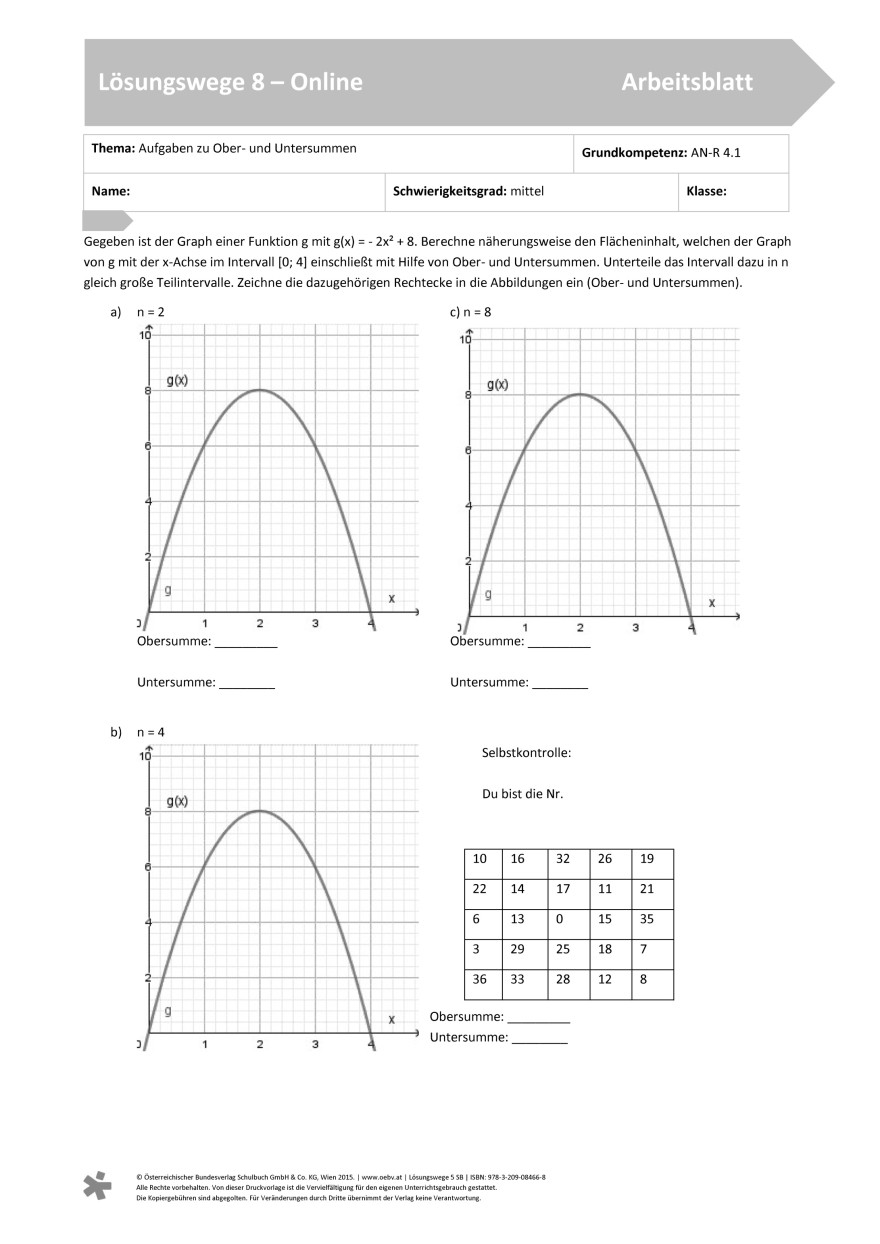

Text erkannt:

Lösungswege 8-Online
Arbeitsblatt
Thema: Aufgaben zu Ober- und Untersummen
Grundkompetenz: AN-R 4.1
Name:
Schwierigkeitsgrad: mittel
Klasse:
Gegeben ist der Graph einer Funktion $g$ mit $g(x)=-2 x^{2}+8$. Berechne näherungsweise den Flächeninhalt, welchen der Graph von $g$ mit der $x$-Achse im Intervall $[0 ; 4]$ einschließt mit Hilfe von Ober- und Untersummen. Unterteile das Intervall dazu in $n$ gleich große Teilintervalle. Zeichne die dazugehörigen Rechtecke in die Abbildungen ein (Ober- und Untersummen).
a) $n=2$
Obersumme:
Untersumme:
b) $n=4$
c) $n=8$
Untersumme:
Selbstkontrolle:
Du bist die $\mathrm{Nr}$.
\begin{tabular}{|l|l|l|l|l|}
\hline 10 & 16 & 32 & 26 & 19 \\
\hline 22 & 14 & 17 & 11 & 21 \\
\hline 6 & 13 & 0 & 15 & 35 \\
\hline 3 & 29 & 25 & 18 & 7 \\
\hline 36 & 33 & 28 & 12 & 8 \\
\hline
\end{tabular}

Obersumme:
Untersumme:
Alle Rechte vorbehalten. Won dieser Druckvorlage ist die Vervieffartigung für den eigenen Unterrichtsgebrauch gestattet.
Die Kopiergebühren sind abgegolten. Für Verinderungen durch Dritte übernimmt der Verlağ beine Verantwortung.

Text erkannt:

Lösungswege 8-Online
Arbeitsblatt
Thema: Aufgaben zu Ober- und Untersummen - Lösungen
Grundkompetenz: AN-R 4.1
Name:
Schwierigkeitsgrad: mittel
Klasse:

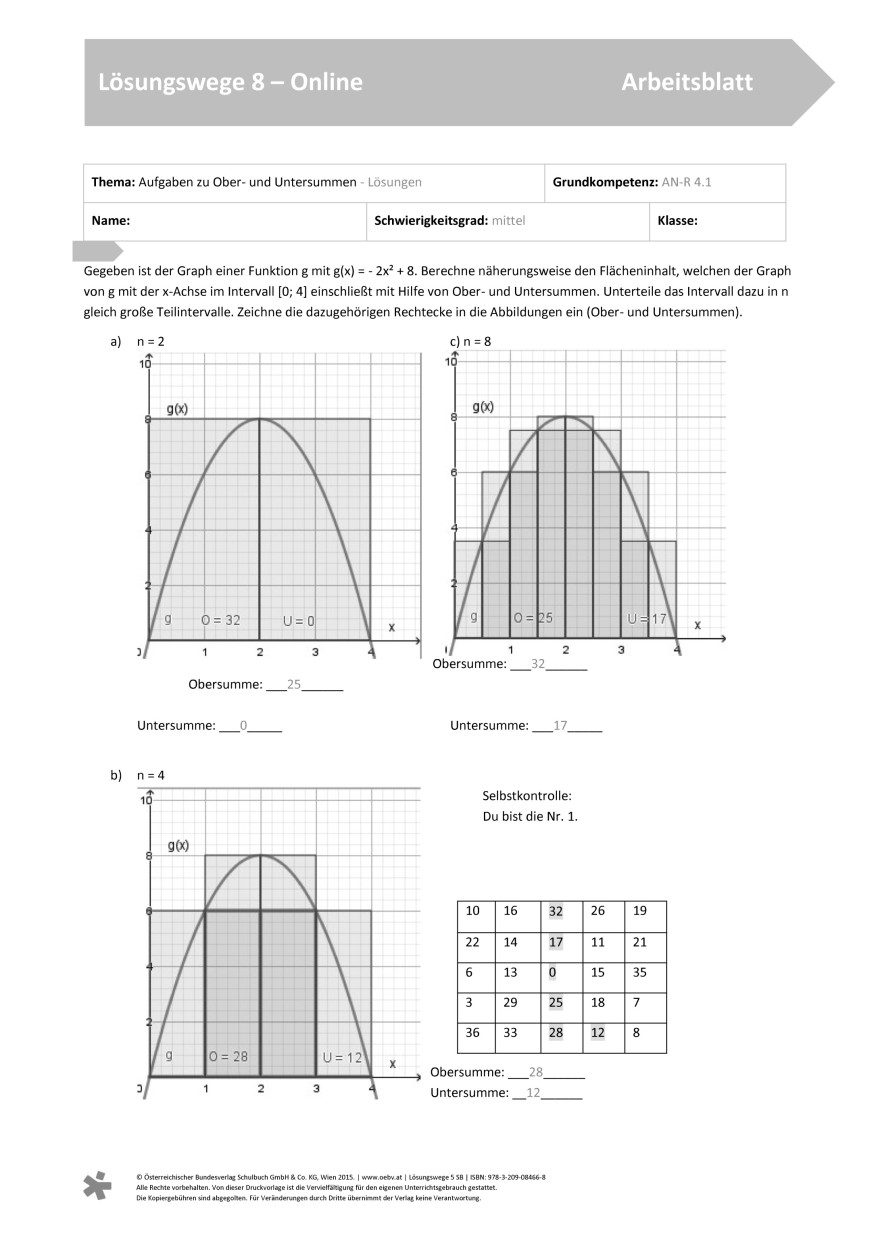
Gegeben ist der Graph einer Funktion $g$ mit $g(x)=-2 x^{2}+8$. Berechne näherungsweise den Flächeninhalt, welchen der Graph von $g$ mit der $x$-Achse im Intervall [0; 4] einschließt mit Hilfe von Ober- und Untersummen. Unterteile das Intervall dazu in $n$ gleich große Teilintervalle. Zeichne die dazugehörigen Rechtecke in die Abbildungen ein (Ober- und Untersummen).
a) $\mathrm{n}=2$
Obersumme: 25
Untersumme: 0
b) $\mathrm{n}=4$
c) $n=8$
Obersumme:
32
Untersumme: 17
Selbstkontrolle:
Du bist die Nr. 1.
\begin{tabular}{|l|l|l|l|l|}
\hline 10 & 16 & 32 & 26 & 19 \\
\hline 22 & 14 & 17 & 11 & 21 \\
\hline 6 & 13 & 0 & 15 & 35 \\
\hline 3 & 29 & 25 & 18 & 7 \\
\hline 36 & 33 & 28 & 12 & 8 \\
\hline
\end{tabular}

Obersumme: 28
Untersumme:_12
Alle Rechte vorbehalten. Von dieser Druckvorlage ist die Vervielfarigung für den eigenen Unterrichtsgebrauch gestattet.
Die Kopiergebühren sind abgegolten. Für Verinderungen durch Dritte übernimmt der Verlağ keine Verantwortung

Answer 1

Die Lösung passt nicht zur Aufgabe, weil der Graph falsch ist.

In der Lösung wird die Funktion $g(x)=-2(x-2)^2+8$ verwendet. Rechne nochmal mit dieser Funktion nach. Ich denke nicht, dass du es nicht verstanden hast, aber falsche Lösungen sind natürlich verwirrend.

Liefere auch deine Rechenwege mit, dann kann leichter nach Fehlern gesucht werden.

Answer 2

Offensichtlich muss die Funktion nicht

g(x) = - 2·x² + 8

sondern

g(x) = - 2·x² + 8·x

lauten. Da erwarte ich von einem Schüler, dass er erkennt das der Scheitelpunkt bei erster Angabe auf der y-Achse liegt und somit nicht richtig sein kann.

Als Nächstes sollte dann die Lehrkraft informiert werden, ob man mit der falsch angegebenen Funktion oder der berichtigten fortfahren soll.

Hier eine Skizze der Rechtecke für die Untersumme mit n = 8