Guten Abend,
Ich hätte eine Frage:
Habe ich die erste Aufgabe a), korrekt gemacht?
Und wie würde ich jetzt b) machen, also wie bestimmt man ein Caushy Produkt?

Text erkannt:
Aufgabe 3: In der Vorlesung wurde das Cauchy-Produkt zweier Reihen \( \sum \limits_{n=0}^{\infty} a_{n} \) und \( \sum \limits_{n=0}^{\infty} b_{n} \) definiert als die Reihe
\( \sum \limits_{n=0}^{\infty} c_{n} \quad \text { mit } \quad c_{n}=\sum \limits_{k=0}^{n} a_{k} b_{n-k} . \)
Sei im Folgenden \( a_{n}=b_{n}=\frac{(-1)^{n+1}}{\sqrt{n+1}} \).
a) Untersuchen Sie die Reihe \( \sum \limits_{n=0}^{\infty} a_{n}=\sum \limits_{n=0}^{\infty} b_{n \Upsilon} \) auf Konvergenz und absolute Konvergenz.
b) Bestimmen Sie das Cauchy-Produkt von \( \sum \limits_{n=0}^{\infty} a_{n} \) und \( \sum \limits_{n=0}^{\infty} b_{n} \).
c) Untersuchen Sie dieses Cauchy-Produkt auf Konvergenz.
Text erkannt:
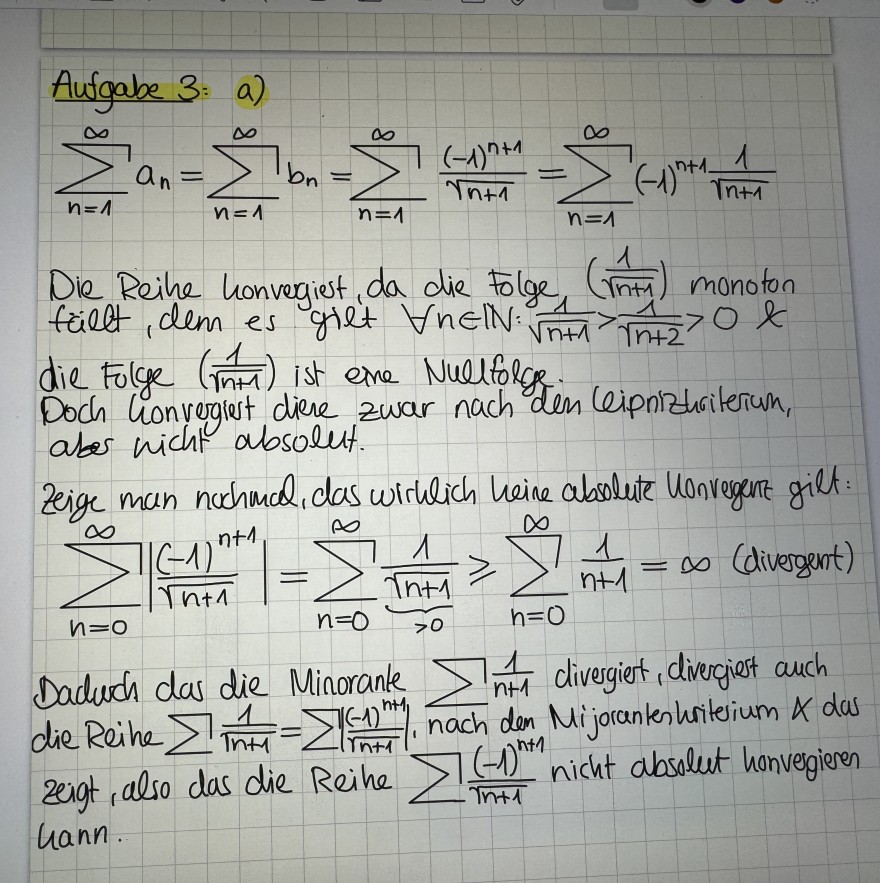
Aufgabe 3: a)
\( \sum \limits_{n=1}^{\infty} a_{n}=\sum \limits_{n=1}^{\infty} b_{n}=\sum \limits_{n=1}^{\infty} \frac{(-1)^{n+1}}{\sqrt{n+1}}=\sum \limits_{n=1}^{\infty}(-1)^{n+1} \frac{1}{\sqrt{n+1}} \)
Die Reihe honvegiest, da die Folge, \( \left(\frac{1}{\sqrt{n+1}}\right) \) monoton fällt, dem es gilt \( \forall n \in \mathbb{N}: \frac{1}{\sqrt{n+1}}>\frac{1}{\sqrt{n+2}}>0 \& \) die Folge \( \left(\frac{1}{\sqrt{n+1}}\right) \) ist eine Nullfolge.
Doch honvergiest diere zwar nach den Ceipnizhriterion, aber nicht absolut.
zeige man nochmal, das wirklich heire absolute Uonveggent gilt:
\( \sum \limits_{n=0}^{\infty}\left|\frac{(-1)^{n+1}}{\sqrt{n+1}}\right|=\sum \limits_{n=0}^{\infty} \frac{1}{\underbrace{\sqrt{n+1}}_{>0}} \geqslant \sum \limits_{n=0}^{\infty} \frac{1}{n+1}=\infty \text { (divergent) } \)
Daduch das die Minorante \( \sum \frac{1}{n+1} \) divergiert, divergiest auch die Reihe \( \sum \frac{1}{\sqrt{n+1}}=\sum \mid \frac{(-1)^{n+1}}{\sqrt{n+1}}, \sum \limits_{\text {nach }} \) den Mijoranten hriterium \( x \) das zeigt, also das die Reihe \( \sum \frac{(-1)^{n+1}}{\sqrt{n+1}} \) nicht absolut honvegieren hann.