Text erkannt:
2 von 3
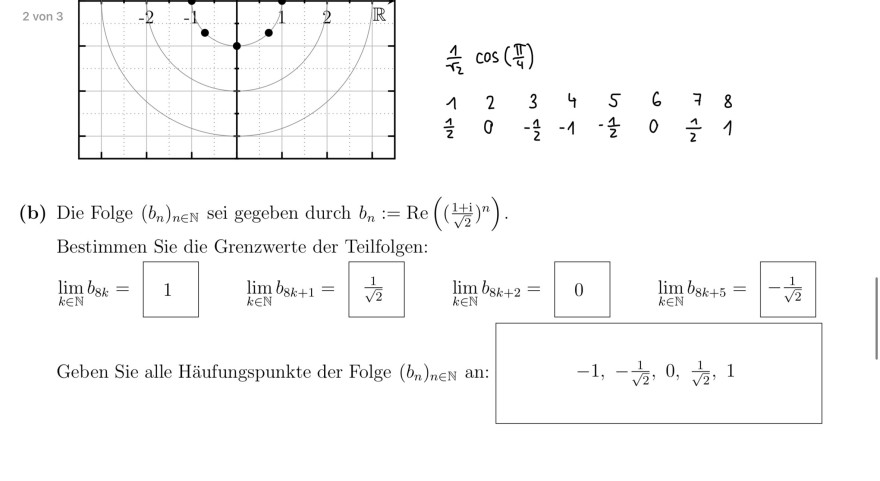
\( \begin{array}{l} \frac{1}{\sqrt{2}} \cos \left(\frac{\pi}{4}\right) \\ \begin{array}{rrrrrrrr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \frac{1}{2} & 0 & -\frac{1}{2} & -1 & -\frac{1}{2} & 0 & \frac{1}{2} & 1 \end{array} \\ \end{array} \)
(b) Die Folge \( \left(b_{n}\right)_{n \in \mathbb{N}} \) sei gegeben durch \( b_{n}:=\operatorname{Re}\left(\left(\frac{1+\mathrm{i}}{\sqrt{2}}\right)^{n}\right) \).
Bestimmen Sie die Grenzwerte der Teilfolgen:
\( \lim \limits_{k \in \mathbb{N}} b_{8 k}=1 \quad \lim \limits_{k \in \mathbb{N}} b_{8 k+1}=\square \frac{1}{\sqrt{2}} \quad \lim \limits_{k \in \mathbb{N}} b_{8 k+2}=\square \quad \lim \limits_{k \in \mathbb{N}} b_{8 k+5}=-\frac{1}{\sqrt{2}} \)
Geben Sie alle Häufungspunkte der Folge \( \left(b_{n}\right)_{n \in \mathbb{N}} \) an:
\( -1,-\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}, 1 \)
Aufgabe:
Bei folgender Aufgabe habe ich mehrere Teilfolgen bestimmt, aber komme leider nicht auf dieses Ergebnis. Auch wenn ich den Betrag mit den einzelnen Folgen multipliziere ist dies nicht die Lösung. Habe ich möglicherweise einen Denkfehler?