Kurvendiskussion von f(x)= e^{1/2x}-1-1/2x und Bestimmung einer Normalen zum Graphen mit der Steigung -0.5

Question

Hier die Aufgabe:

Gegeben ist die Funktion f mit f(x)= e^1/2x-1-1/2x ; X Element R

K ist das Schaubild von f

1. Wie bestimme ich den Schnittpunkt mit der y-Achse?

2. Wie untersuche ich K auf Hoch- Tief- und Wendepunkte und Asymptoten?

3. Wie finde ich heraus, wo K die Steigung 3/2 hat?

4. In welchem Kurvenpunkt P ist die Normale von K parallel zur Geraden mit der Gleichung y=-1/2x+3?

Und wie bestimme ich die Abszisse von P?

Comments

Es ist nicht ganz klar wo die x stehen. Das erste vermutlich im Exponenten (unter dem Bruchstrich oder daneben?)  und das zweite auf welcher Höhe? -1 ist nicht im Exponenten. oder?

Falls x unter einem Bruchstrich, so ist f(0) gar nicht definiert

f(x)= e^{1/2x}-1-1/2x            würde dann die y-Achse gar nicht schneiden.

Answer 1

Gegeben ist die Funktion f mit f(x)= e^{1/2x}-1-1/2x ; X Element R

Ich nehme mal an, dass die einfachst denkbare Funktion vorliegt:

f(x) = e^{0.5x} - 1 - 0.5x

f ' (x) = 0.5 e^{0.5x} - 0.5 

3. Wie finde ich heraus, wo K die Steigung 1.5 hat?

1.5 = 0.5 e^{0.5x} - 0.5 

2 = 0.5 e^{0.5x} 

4 = e^{0.5x}

ln (4) = 0.5 x

2*ln(4) = x

y  = e^{0.5x} - 1 - 0.5x =  e^{0.5*2*ln 4} - 1 - 0.5*2*ln(4)

=e^{ln 4} - 1 - ln(4)

= 4 -1 -ln(4) = 3 - ln(4) ==> In P (2*ln(4)| 3- ln(4)) ist die Steigung 1.5

4. In welchem Kurvenpunkt P ist die Normale von K parallel zur Geraden mit der Gleichung y=-1/2x+3?

Hier muss die momentane Steigung (Ableitung) f ' (x) = - 1 / (-0.5) = 2 sein.

Also 2 = 0.5 e^{0.5x} - 0.5 

2.5 = 0.5 e^{0.5x}

5 = e^{0.5x}

ln (5) = 0.5 x

2 ln (5) = x

 

y  = e^{0.5x} - 1 - 0.5x =  e^{0.5*2*ln 5} - 1 - 0.5*2*ln(5)

=e^{ln 5} - 1 - ln(5)

= 5 -1 -ln(5) = 4 - ln(5) ==> In P (2*ln(5)| 4- ln(5)) verläuft die Normale zur Kurve parallel zur gegebenen Geraden.

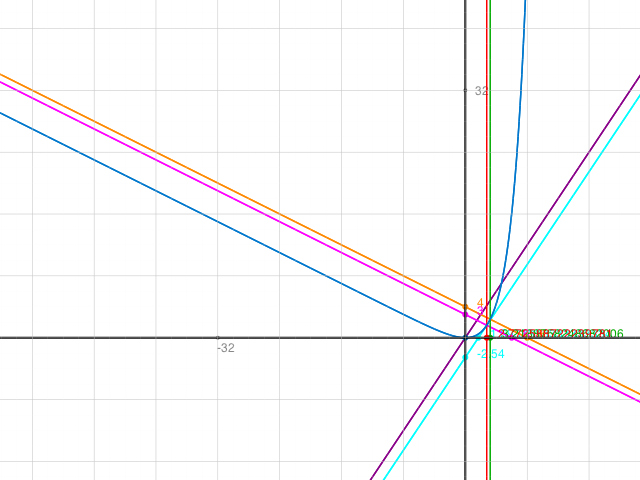
Skizze: Blau: Kurve. Rot x=2*ln (4). Grün x=2*ln (5). Gelb: gesuchte Normale parallel zu Lila. Türkis: Tangente mit Steigung 1.5 parallel zur violetten Geraden.

 

 

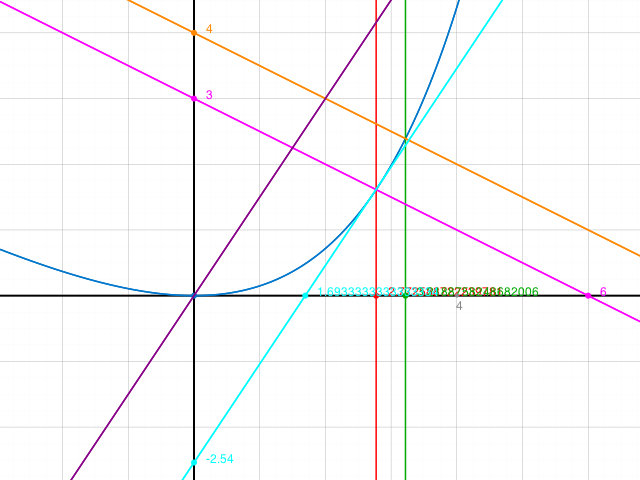
In diesem Zoom sieht man, wo die Nullstelle und das relative Minimum liegen. Wendepunkt und rel. Maximum gibt's nicht.

Anleitung zu deren Berechnung:
Nullstelle: f(x) =0 setzen und feststellen, dass e^0 = 1. --> P(0/0)
f ' (x) = 0 setzen : -> x=0 → P(0/0) relatives Minimum. 

und f ' ' (x) = 0 → keine Lösung.