Vom Duplikat:
Titel: Berechnen Sie, wie viel m² Glas benötigt werden!
Stichworte: parabel,funktion
Aufgabe:
Ein Kirchenfenster wird oben durch die Funktion f(x) = -x² + 10x - 17 begrenzt,
x undf f(x) in Metern. Berechnen Sie, wie viel m² Glas benötigt werden! mit Koordinatensystem:
In der Datei ist auch das Koordinatensystem mit dem Graphen eingefügt. Ich hoffe man kann alles erkennen und jemand kann mir helfen.
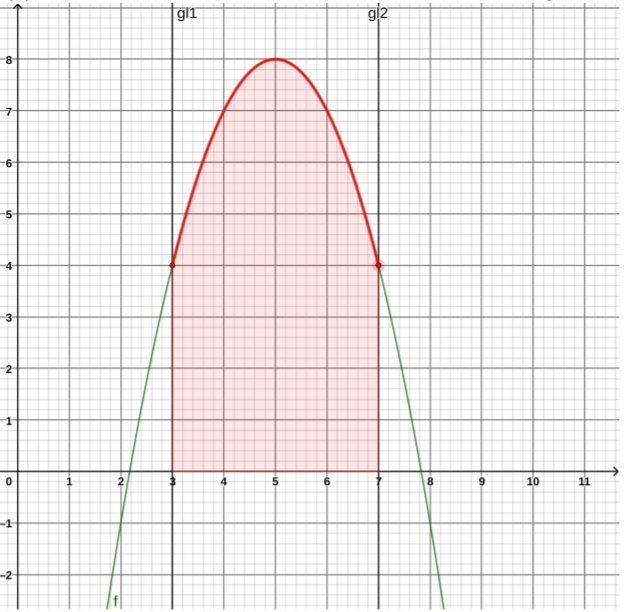
Problem/Ansatz:
Ich brauche wirklich Hilfe bei der Aufgabe. Ich sitze wirklich seit Stunden dran verstehe leider aber fast nichts. Ich muss die Aufgabe rechnen und präsentieren können vor der gesamten Klasse und die Präsentation macht ganze 30% meiner Note aus, da ich sowieso schon schlecht in Mathe stehe würde mir das sehr helfen.