Question

Bildet die folgenden Menge zusammen mit der üblichen Addition und Skalaren Multiplikation einen Vektorraum über dem Körper der reellen Zahlen?

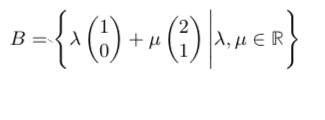
Text erkannt:

\( B=\left\{\lambda\left(\begin{array}{l}1 \\ 0\end{array}\right)+\mu\left(\begin{array}{l}2 \\ 1\end{array}\right) \mid \lambda, \mu \in \mathbb{R}\right\} \)

Answer 1

Ja, man kann ja die Vektorraumaxiome nachprüfen aber in diesem Fall wäre der Vektorraum einfach der R^2.

                

Answer 2

Prüfe die Axiome nach. Woran scheitert es denn?