WK zuerst alle Karten der einen Farbe und dann alle Karten der anderen Farbe?

Question

Aufgabe:

Ein Kartenspiel besteht aus 5 weißen und 7 schwarzen Karten.

a) Alle Karten werden nacheinander ohne Zurücklegen gezogen. Mit welcher Wahrscheinlichkeit erhält man
zuerst alle Karten der einen Farbe und dann alle Karten der anderen Farbe?

Lösung: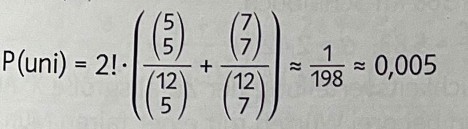

Text erkannt:

\( P( \) uni \( )=2 ! \cdot\left(\frac{\left(\begin{array}{l}5 \\ 5\end{array}\right)}{\left(\begin{array}{c}12 \\ 5\end{array}\right)}+\frac{\left(\begin{array}{l}7 \\ 7\end{array}\right)}{\left(\begin{array}{c}12 \\ 7\end{array}\right)}\right) \approx \frac{1}{198} \approx 0,005 \)

Problem/Ansatz:

Ich verstehe nicht weshalb 2!.

Grundsätzlich habe ich das Problem in der Kombinatorik die Möglichkeiten

mit den WK in Verbindung zu bringen um ein Ereignis zu berechnen.

Also ich denke mal das die 2! die Möglichkeiten darstellen sollen aber weiß nicht wie man darauf kommt.

Ich habe es mit einem Baumdiagramm berechnet indem ich alle Karten der Farbe schwarz gelegt habe und daraufhin die der weißen. Das habe ich dann auch andersrum gemacht und kam insgesamt aufs gleiche Ergebnis.

Allerdings kann ich aus dem Baumdiagramm kein Zusammenhang finden zu dieser Lösungsvariante also weshalb die 2!.

Answer 1

a) Alle Karten werden nacheinander ohne Zurücklegen gezogen. Mit welcher wahrscheinlichkeit erhält man zuerst alle Karten der einen Farbe und dann alle Karten der anderen Farbe?

Der Faktor 2 ist verkehrt

P(Die ersten 5 Karten sind weiß oder die ersten 7 Karten sind schwarz)

= P(wwwww..., sssssss...)

= 5/12*4/11*3/10*2/9*1/8 + 7/12*6/11*5/10*4/9*3/8*2/7*1/6

= 1/792 + 1/792

= 1/396

Du hättest aber auch nur die Wahrscheinlichkeit dass die ersten 5 Karten weiß sind und diese Wahrscheinlichkeit mal 2 nehmen können, weil es die gleiche Wahrscheinlichkeit ist als wenn die letzten 5 Karten weiß sind.

P(wwwww..., ...wwwww)

= 2 * 5/12*4/11*3/10*2/9*1/8

= 2 * 1/792

= 1/396

Aber den Faktor 2 nehmen und trotzdem die beiden Pfade addieren ist verkehrt.

Answer 2

Es gibt nur 2 gesuchte Möglichkeiten/ Ergebnisse/günstige Ausgänge

wwwwwsssssss, ssssssswwwww

Anzahl aller möglichen Ergebnisse:

12!(5!*7!) = 792 ( Permutation mit Wh)

-> P = 2/792 = 1/396