Zugehörigen n Wert WK gleiche Farbe

Question

Aufgabe:

Text erkannt:

In einem Behälter \( B_{1} \) befinden sich fünf rote Kugeln, in einem zweiten Behälter \( B_{2} \) zwei rote Kugeln und eine unbekannte Anzahl \( n \) blauer Kugeln, wobei \( n>1 \) gilt.

Aus dem Behälter \( B_{2} \) wird eine Kugel zufällig entnommen und in den Behälter \( B_{1} \) gelegt.
a Angenommen, die Wahrscheinlichkeit dafür, dass nun in einem der Behälter ausschließlich Kugeln derselben Farbe liegen, beträgt \( \frac{1}{5} \). Bestimmen Sie den zugehörigen Wert von \( \mathrm{n} \) und beschreiben Sie Ihren Gedankengang.

Problem/Ansatz:

ich habe keine Idee für einen Ansatz. Außer dass P(Behälter hat nur rote) + P(Behälter hat nur blaue Kugeln) = 1/5

Answer 1

Wenn in einem Behälter nur Kugeln einer Farbe sein dürfen, dann muss das Behälter B1 sein mit nur roten Kugeln. Das bedeutet man muss von B2 eine rote Kugel nach B1 gelegt haben und die Wahrscheinlichkeit muss gleich 1/5 gewesen sein.

2/(2 + n) = 1/5 --> n = 8

Damit müssen in B2 8 blaue Kugeln sein.

Comments

Angenommen, die Wahrscheinlichkeit dafür, dass nun in einem der Behälter ausschließlich Kugeln derselben Farbe liegen, beträgt \( \frac{1}{5} \).

Ein seltsamer Satz: Es geht um die WKT des Behälterinhalts, nicht einzelner Kugeln. Wie soll man ihn verstehen?

---

Wie soll man ihn verstehen?

So wie er dort steht.

Answer 2

Hallo

nur eine Farbe ist ja nicht möglich  da in B2 2 rote K und mindestens 2 blaue liegen, also muss man au B2 eine rote Kugel ziehen. wie groß muss dann die Anzahl der blauen sein?

lul

Comments

Text erkannt:

B
\( B_{n}:\left(\begin{array}{lll}r & r & r \\ r & r & r \\ 2 & \end{array}\right) \)
\( B_{2} \) :
danit \( \frac{1}{5}=P( \) nar rot)

Irgendwie komme ich nicht darauf.

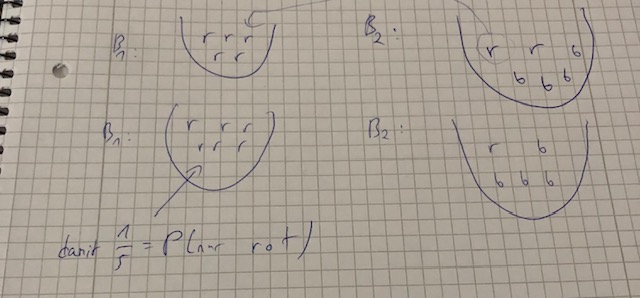
Also bis hierhin verstehe ich es. Es muss eine rote Kugel zu B1 gelegt werden, damit P(nur gleiche Farbe in einem Behälter) = 1/5 gilt.

und weil falls n für die blauen Kugel 2 wäre, diese nicht zu B1 darf weil sonst wäre n=1 soll aber n>1 sein.

In B1 sind dann 6 rote und 1 rote bei B2...

aber wie komme ich jetzt auf die Anzahl von den blauen Kugeln?

Habe 4 blaue als Beispiel hingezeichnet..

---

Bei 4 blauen Kugeln ist die Wahrscheinlichkeit

2/(2 + 4) = 2/6 = 1/3 eine rote Kugel von B2 nach B1 zu legen und nicht 1/5. Es soll aber genau 1/5 sein oder?