Question

Bestimmen Sie die Fläche, die der Graph f(x) = 4 - ( 2 / ( x^2 ) ), Df = R{0}, x-Achse und die Gerade g(x) = -4 einschließen.

Answer 1

Es geht um den Inhalt der grün markierten Fläche.

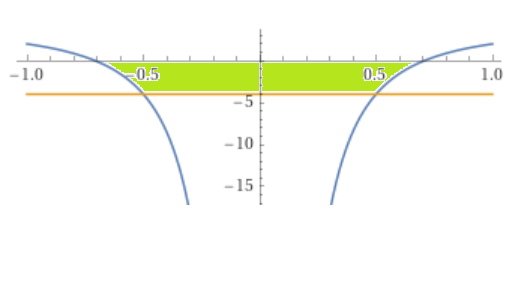
Wenn von links nach rechts a und d die beiden Nullstellen von f(x) sind und b und c die Stellen wo f(x) = -4, dann ist der Inhalt der Fläche

\(\displaystyle A= \int\limits_{a}^{b} - (4 - ( 2 / ( x^2 ) ) \, dx + (c-b) \cdot 4 + \int\limits_{c}^{d} - (4 - ( 2 / ( x^2 ) ) \, dx \)

Answer 2

Gerichteter Flächeninhalt A

$$A = 2 \cdot\left(\int \limits_{0}^{1 / 2}-4 ~ \mathrm{dx}+\int \limits_{1 / 2}^{\sqrt{2}/2}\left(4-\frac{2}{x^2}\right) \mathrm{dx}\right) = 8·√2 - 16 \approx -4.686$$

Der Flächeninhalt beträgt ca. 4.686 FE.

Comments

Der Flächeninhalt beträgt ca. 0.8284 FE.

Der Flächeninhalt beträgt ca. 4,7

---

Der Flächeninhalt beträgt ca. 4,7

Danke für die Richtigstellung. Ich habe den Tippfehler in der Rechnung und das Ergebnis korrigiert.